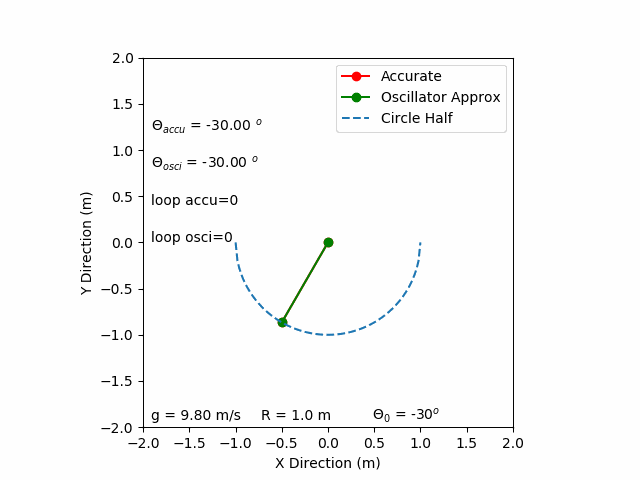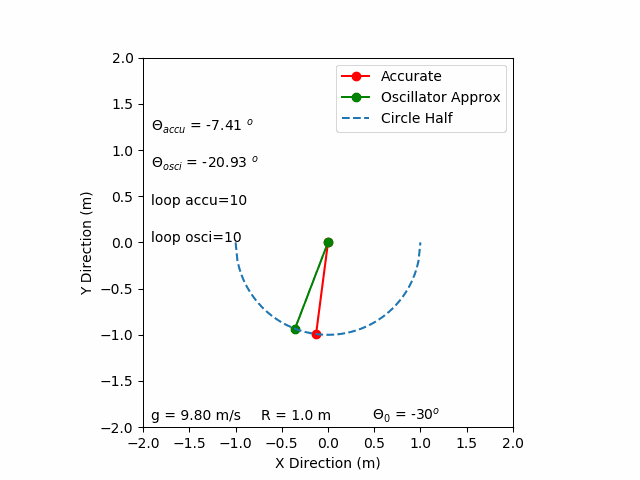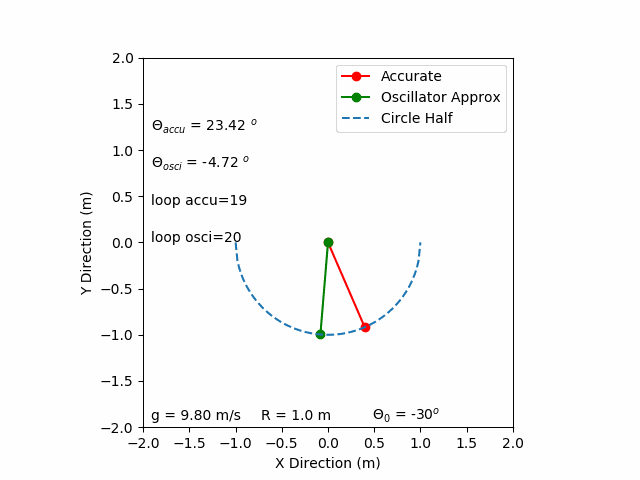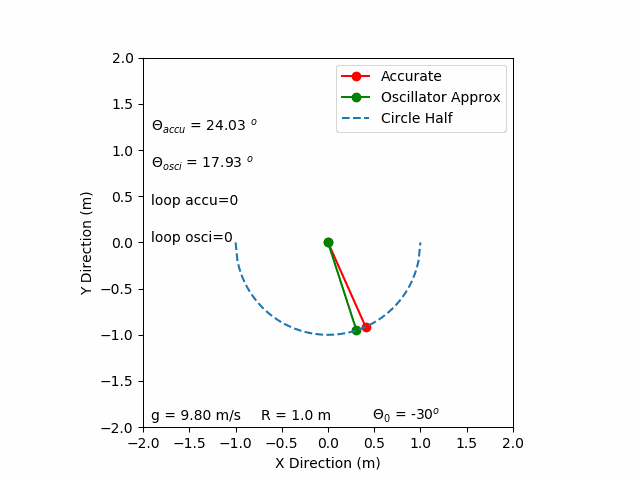
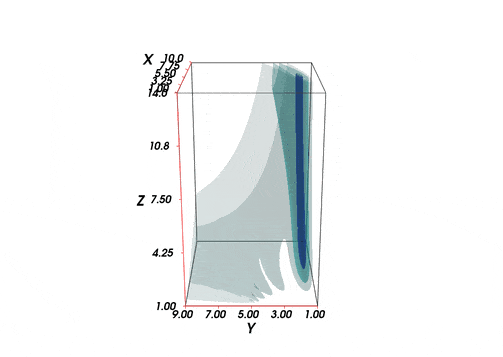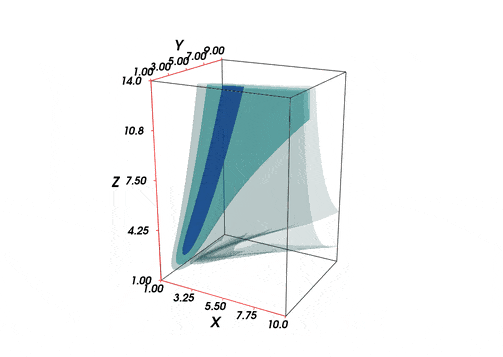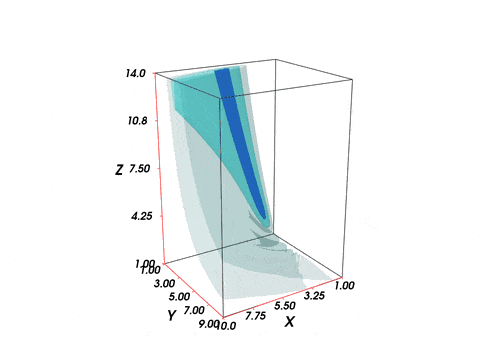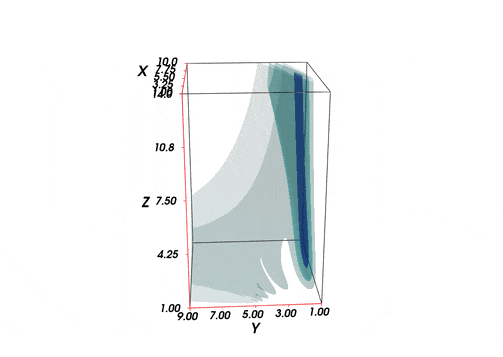
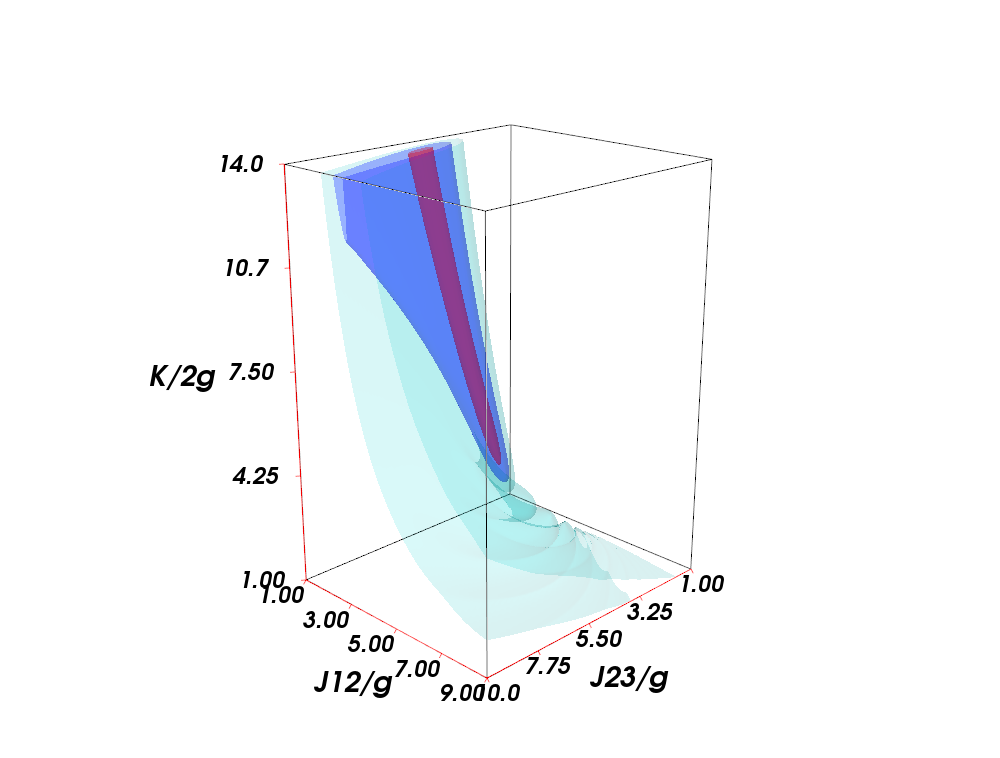
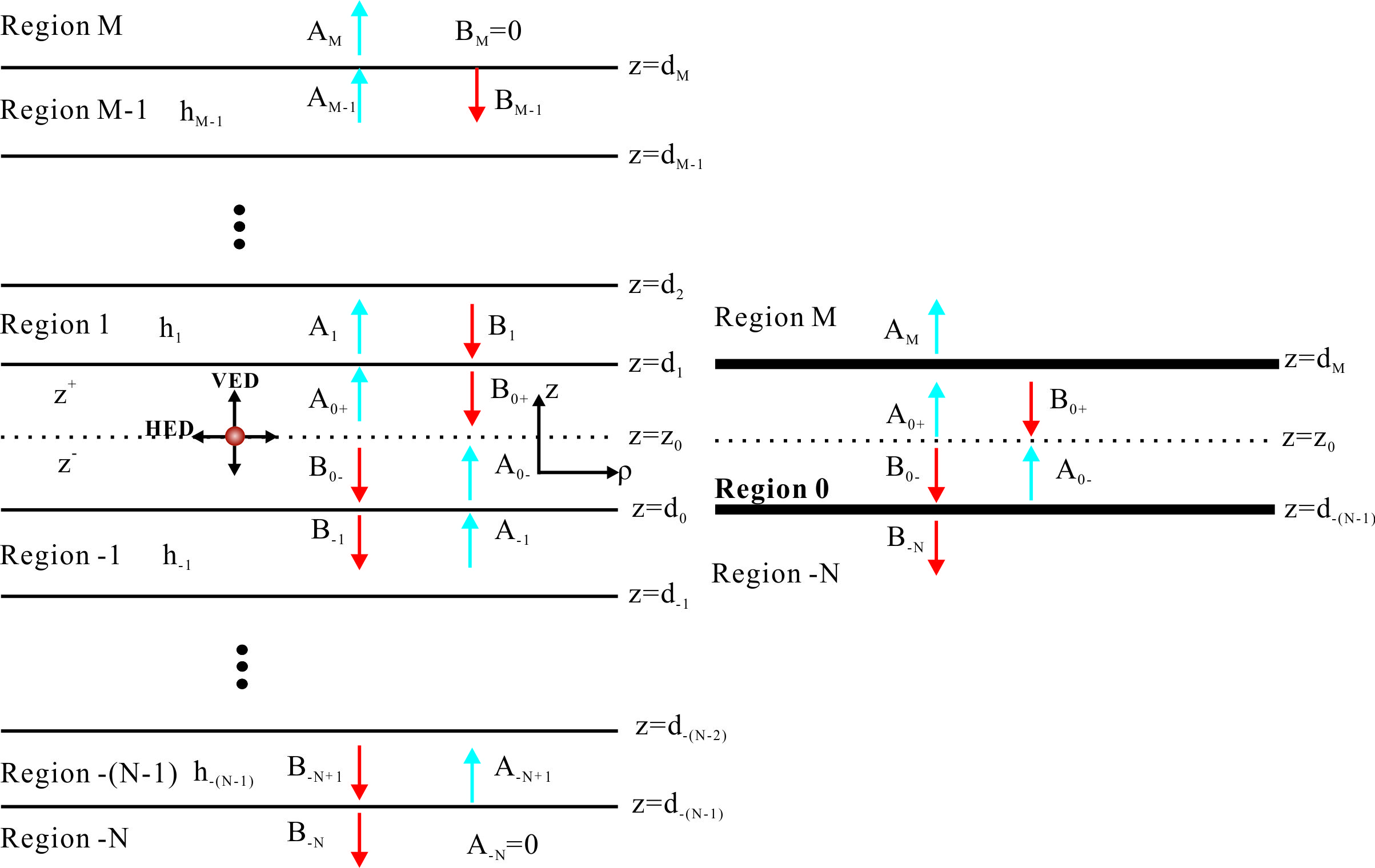
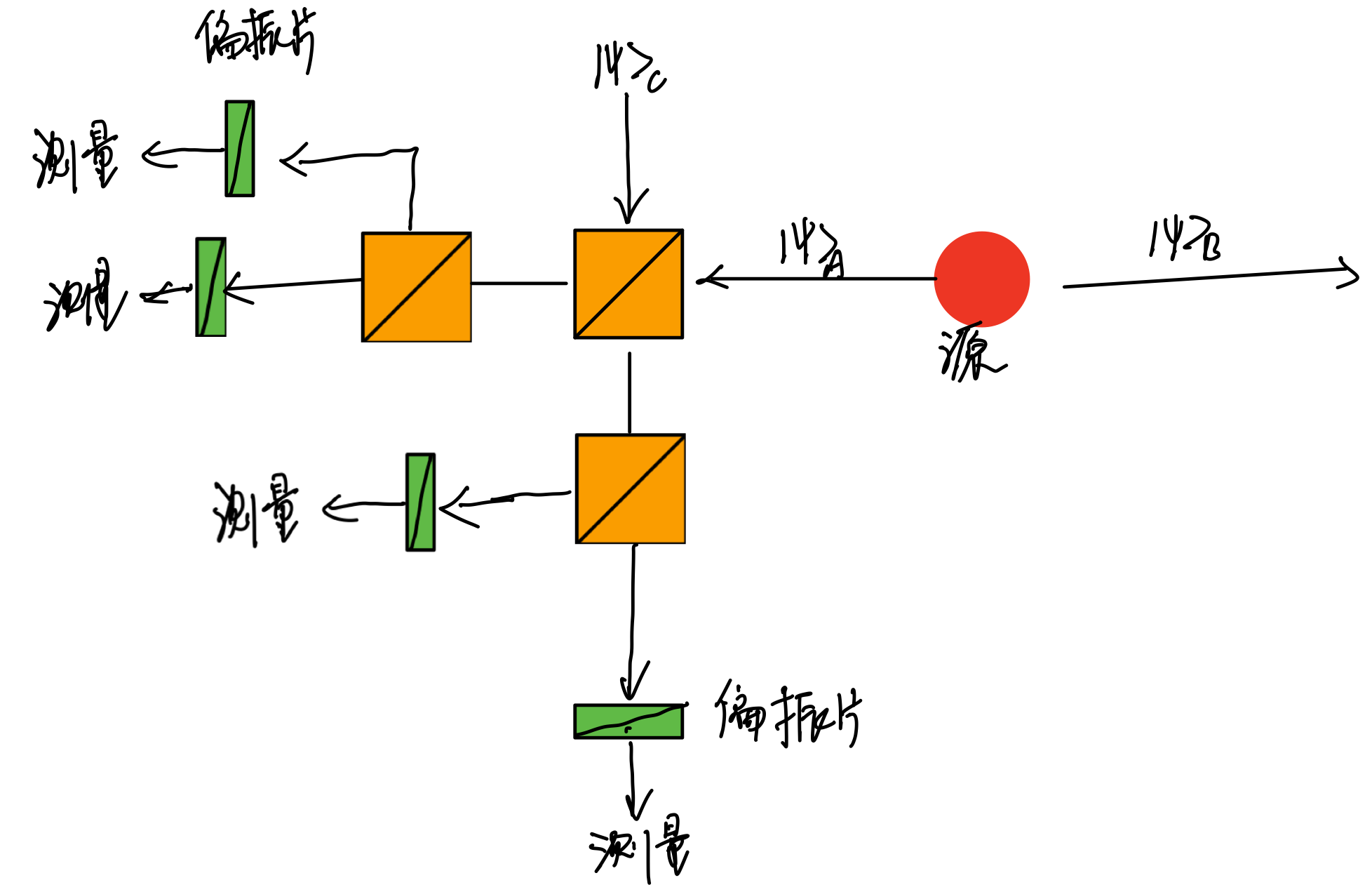
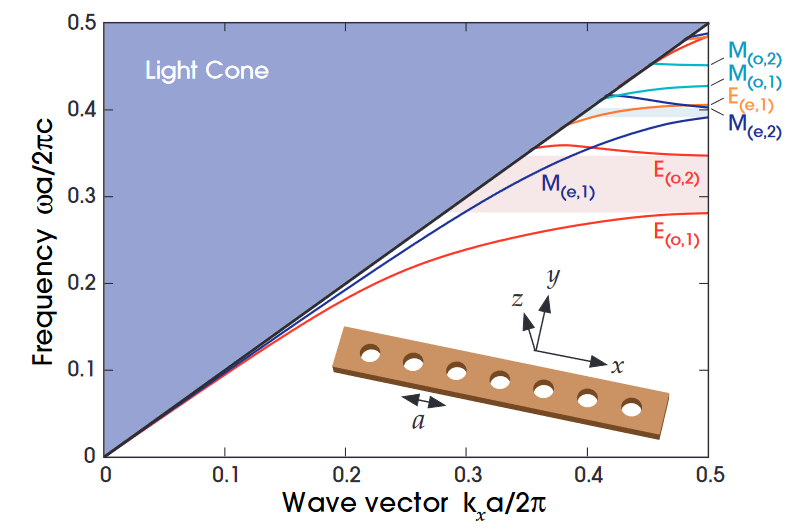
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
|
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
from scipy.integrate import odeint
theta_0 = -np.pi/6
theta_0_degree = theta_0/np.pi*180
R = 1.0
g = 9.8
coe = 1
def evo_accu(z, t, g, R, coe):
v = z[0]
theta = z[1]
dtheta = v/R
dv = -coe*g*np.sin(theta)
dzdt = [dv, dtheta]
return dzdt
def evo_osci(z, t, g, R, coe):
v = z[0]
theta = z[1]
dtheta = v/R
dv = -coe*g*theta
dzdt = [dv, dtheta]
return dzdt
t_max = 1.0/R*g*3
numt = 500
tmat = np.linspace(0, t_max, numt)
z0 = [0, theta_0]
theta_accu = odeint(evo_accu, z0, tmat, args=(g, R, coe))
theta_osci = odeint(evo_osci, z0, tmat, args=(g, R, coe))
x_accu = R*np.sin(theta_accu[:, 1])
y_accu = -R*np.cos(theta_accu[:, 1])
x_osci = R*np.sin(theta_osci[:, 1])
y_osci = -R*np.cos(theta_osci[:, 1])
theta_accu_degree = theta_accu[:, 1]/np.pi*180
theta_osci_degree = theta_osci[:, 1]/np.pi*180
x_cir = np.linspace(-R, R, 100)
y_cir = -np.sqrt(R**2-x_cir**2)
count_accu = np.zeros(numt)
count_osci = np.zeros(numt)
counter_accu = 0
counter_osci = 0
for i in range(numt-1):
if(theta_accu[i, 1]*theta_accu[i+1, 1] < 0):
counter_accu = counter_accu+1
count_accu[i] = counter_accu
else:
count_accu[i] = counter_accu
if(theta_osci[i, 1]*theta_osci[i+1, 1] < 0):
counter_osci = counter_osci+1
count_osci[i] = counter_osci
else:
count_osci[i] = counter_osci
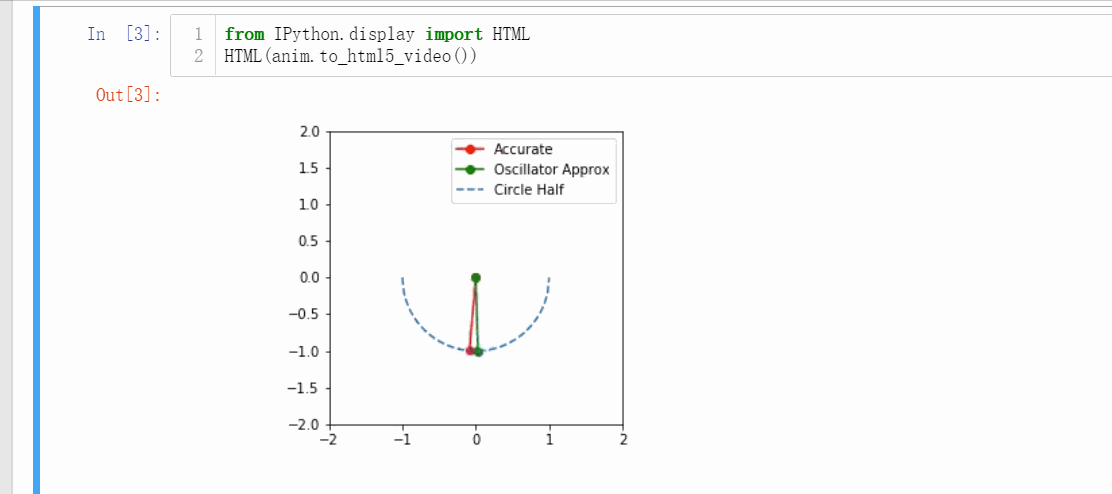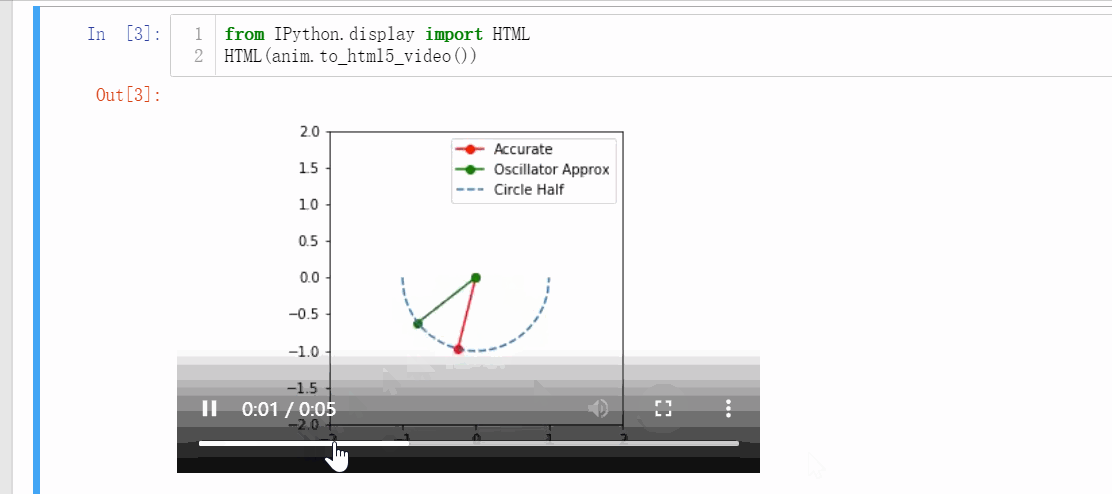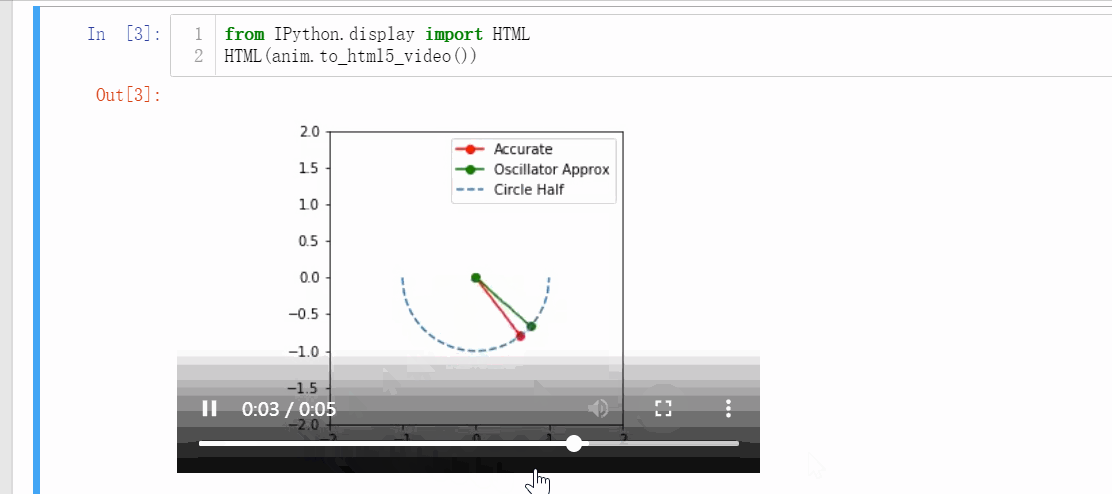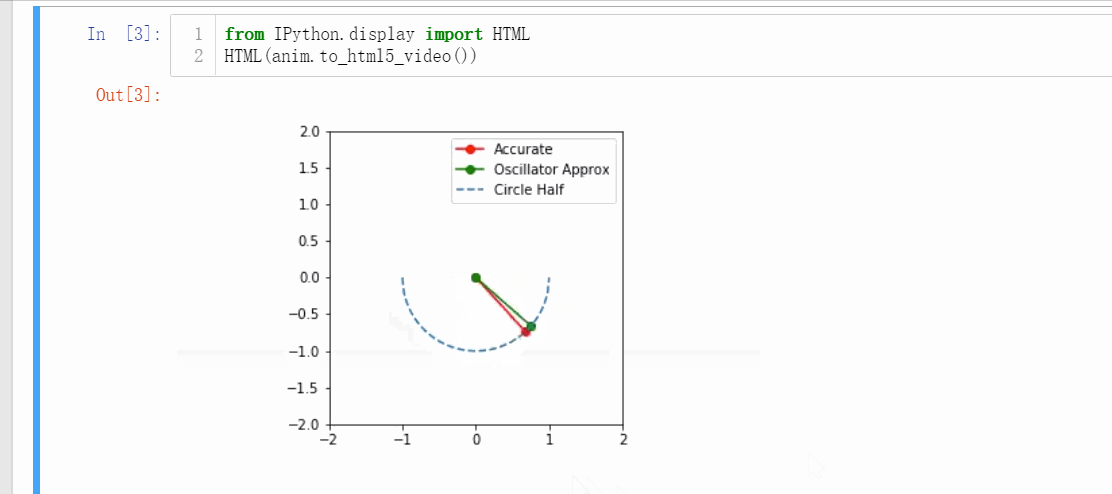
fig = plt.figure()
ax = plt.axes(xlim=(-2, 2), ylim=(-2, 2), aspect='equal')
line_accu, = ax.plot([], [], 'r-o', label='Accurate')
line_osci, = ax.plot([], [], 'g-o', label='Oscillator Approx')
theta_accu_text = ax.text(0.02, 0.8, '', transform=ax.transAxes)
theta_osci_text = ax.text(0.02, 0.7, '', transform=ax.transAxes)
loop_accu_text = ax.text(0.02, 0.6, '', transform=ax.transAxes)
loop_osci_text = ax.text(0.02, 0.5, '', transform=ax.transAxes)
line_cir, = ax.plot(x_cir, y_cir, '--', label='Circle Half')
def init():
line_accu.set_data([], [])
line_osci.set_data([], [])
theta_accu_text.set_text('')
theta_osci_text.set_text('')
loop_accu_text.set_text('')
loop_osci_text.set_text('')
return line_accu, line_osci, theta_accu_text, theta_osci_text, loop_accu_text, loop_osci_text,
def animate(i):
x_accu_mat = [0, x_accu[i]]
y_accu_mat = [0, y_accu[i]]
x_osci_mat = [0, x_osci[i]]
y_osci_mat = [0, y_osci[i]]
line_accu.set_data(x_accu_mat, y_accu_mat)
line_osci.set_data(x_osci_mat, y_osci_mat)
theta_accu_text.set_text(
'$ \Theta_{accu} $ = %.2f $^o $' % theta_accu_degree[i])
theta_osci_text.set_text(
'$ \Theta_{osci} $ = %.2f $^o $' % theta_osci_degree[i])
loop_accu_text.set_text('loop accu=%.1d' % count_accu[i])
loop_osci_text.set_text('loop osci=%.1d' % count_osci[i])
return line_accu, line_osci, theta_accu_text, theta_osci_text, loop_accu_text, loop_osci_text,
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=numt, interval=10, blit=False)
plt.legend(loc='best')
plt.xlabel('X Direction (m)')
plt.ylabel('Y Direction (m)')
ax.text(0.02, 0.02, 'g = %.2f m/s' % g, transform=ax.transAxes)
ax.text(0.32, 0.02, 'R = %.1f m' % R, transform=ax.transAxes)
ax.text(0.62, 0.02, '$\Theta_{0}$ = %.1d$^o $' %
theta_0_degree, transform=ax.transAxes)
anim.save("Ball_1.gif", writer='pillow')
|