Python #Plot

All the python study code can be found in my own repository.

Purpose

When we describe the angle of an vector in 3d space, we will use three vectors to describe them. When We have three orthogonal vectors, how can be describe them and show them via plot? This is the purpose of this note.

To plot three orthogonal vectors in a 3d space. We will use three parameters to describe them.

  1. : the polar angle, angle between the c axis and the z axis
  2. : the azimuthal angle
  3. Ratio_xy : to rotate the other two orthogonal vectors

I will begin from the special c-axis and it can be described by the polar angle and the azimuthal angle . The two other vectors are in the plane orthogonal to c-axis they can rotate in the plane. We can describe them via a ratio . The three vectors can be expressed as

where the are used to express the normalized vectors. It’s easy to check that the three vectors defined above are orthogonal to each other.

Results

,ratio_xy=1

view 1

view 2

,ratio_xy=10

view 1

view 1

The code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
# To show the incident angle in 3D axis
# Date: 2019 08 03
# Authour: Zhaohua Tian

# Import necessary libraries
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.patches import FancyArrowPatch
from mpl_toolkits.mplot3d import proj3d

theta = np.pi / 6
phi = np.pi / 4


class Arrow3D(FancyArrowPatch):

    def __init__(self, xs, ys, zs, *args, **kwargs):
        FancyArrowPatch.__init__(self, (0, 0), (0, 0), *args, **kwargs)
        self._verts3d = xs, ys, zs

    def draw(self, renderer):
        xs3d, ys3d, zs3d = self._verts3d
        xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
        self.set_positions((xs[0], ys[0]), (xs[1], ys[1]))
        FancyArrowPatch.draw(self, renderer)


# Prepare the coordinate matrix
num_arrow = 3
coor0 = np.zeros((1, 3))
row = np.ones((num_arrow, 1))
coor = np.matmul(row, coor0)
x = np.cos(theta) * np.sin(phi)
y = np.cos(theta) * np.cos(phi)
z = np.sin(theta)

ar_1 = np.array([x, y, z])
nar_1 = ar_1 / np.sqrt(ar_1[0] ** 2 + ar_1[1] ** 2 + ar_1[2] ** 2)

ratio_xy = 10
ar_2 = np.array([1, ratio_xy, -y / z * ratio_xy - x / z])
nar_2 = ar_2 / np.sqrt(ar_2[0] ** 2 + ar_2[1] ** 2 + ar_2[2] ** 2)

nar_3 = np.cross(nar_1, nar_2)

# To plot the projection of nar_1
num = 20
x_mat = np.linspace(-1, 1, num)
z_mat = np.linspace(0, 1, num)
line_1_xy = np.array([(z_mat)*x, (z_mat)*y, (z_mat)*0])
line_1_z = np.array([np.ones(num)*x, np.ones(num)*y, (z_mat)*z])

# To  plot the x,y,z coordinate
line_x = np.array([x_mat, x_mat*0, x_mat*0])
line_y = np.array([x_mat*0, x_mat, x_mat*0])
line_z = np.array([x_mat*0, x_mat*0, x_mat])

# To plot the xy plane
xx, yy = np.meshgrid(x_mat, x_mat)
zz_xy = np.zeros((num, num))
# to plot the orthogonal plane
zz_or = (-x*xx-y*yy)/z
# To plot the \theta \phi
theta_x = z_mat*x*0.5
theta_y = z_mat*y*0.5
theta_z = np.sqrt(0.25-theta_x**2-theta_y**2)

phi_y = np.linspace(0, y, num)
phi_x = np.sqrt(x**2+y**2-phi_y**2)
phi_z = np.zeros(num)
# Plot part
# Plot the arrow
fig = plt.figure()
ax = fig.gca(projection='3d')


# Three arrows
a1 = Arrow3D([0, nar_1[0]], [0, nar_1[1]], [0, nar_1[2]], mutation_scale=20,
             lw=2, arrowstyle="-|>", color="r")
ax.add_artist(a1)

a2 = Arrow3D([0, nar_2[0]], [0, nar_2[1]], [0, nar_2[2]], mutation_scale=20,
             lw=1, arrowstyle="-|>", color="b")
ax.add_artist(a2)

a3 = Arrow3D([0, nar_3[0]], [0, nar_3[1]], [0, nar_3[2]], mutation_scale=20,
             lw=1, arrowstyle="-|>", color="b")
ax.add_artist(a3)
# The projection
a4 = ax.plot(line_1_xy[0, :], line_1_xy[1, :], line_1_xy[2, :], 'k--')
a5 = ax.plot(line_1_z[0, :], line_1_z[1, :], line_1_z[2, :], 'k--')

# The x,y,z coordinate
ax_x = ax.plot(line_x[0, :], line_x[1, :], line_x[2, :], 'k--')
ax_y = ax.plot(line_y[0, :], line_y[1, :], line_y[2, :], 'k--')
ax_z = ax.plot(line_z[0, :], line_z[1, :], line_z[2, :], 'k--')
# The xy plane
surf_xy = ax.plot_surface(xx, yy, zz_xy, alpha=0.3, color=(0, 0, 1))
# The orthogonal plane
surf_or = ax.plot_surface(xx, yy, zz_or, alpha=0.3, color=(0, 0, 1))
# The theta angle
theta_angle = ax.plot(theta_x, theta_y, theta_z, 'r-')
# The phi angle
phi_angle = ax.plot(phi_x, phi_y, phi_z, 'r-')

ax.set_xlim((-1, 1))
ax.set_ylim((-1, 1))
ax.set_zlim(-1, 1)
ax.text(0, 0, 1, 'z')
ax.text(1, 0, 0, 'x')
ax.text(0, 1, 0, 'y')
ax.text(x, y, z, 'c axis')
ax.text(theta_x[10], theta_y[10], theta_z[10], '$\\theta$')
ax.text(phi_x[10], phi_y[10], phi_z[10], '$\\phi$')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
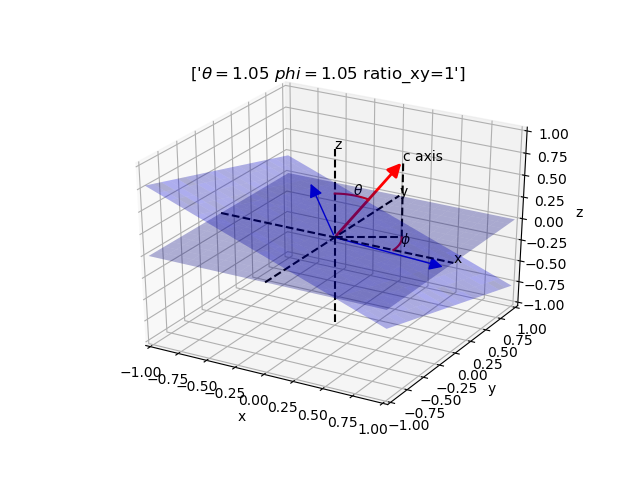
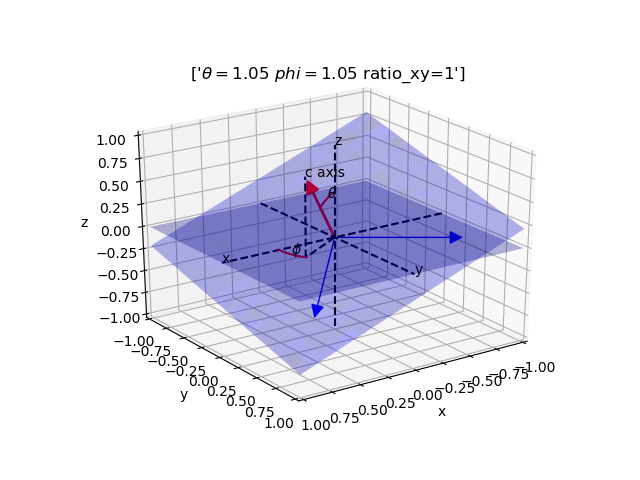
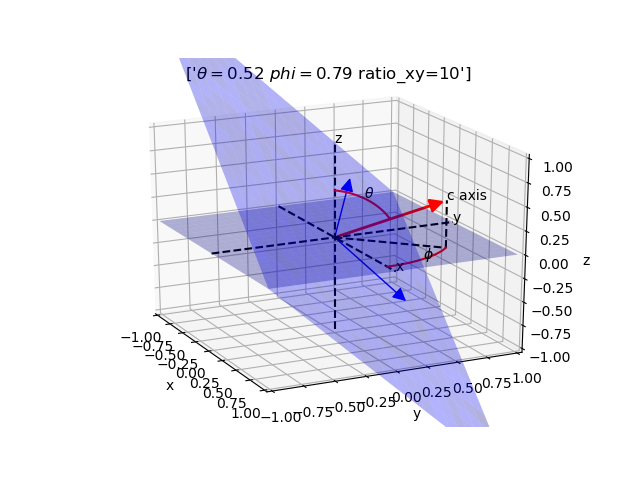
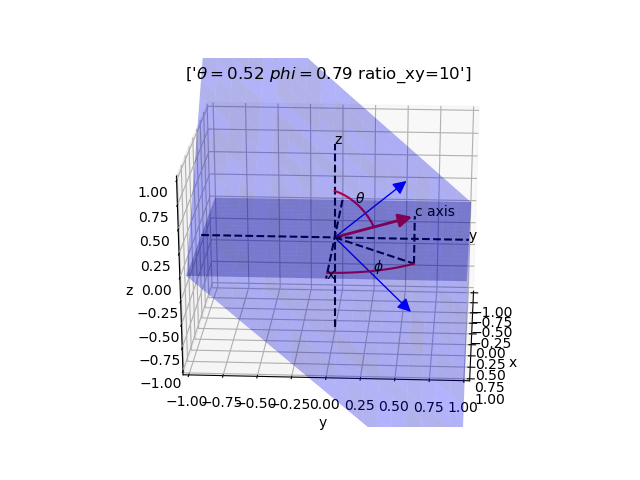
ax.set_title(['$\theta = $' + str(round(theta, 2))+' '+'$ phi = $' +
              str(round(phi, 2))+' '+'ratio_xy=' + str(round(ratio_xy, 2))])
plt.show()