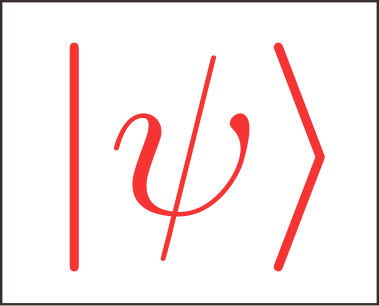Meep教程(5) MPB计算光子晶体波导能带
教科书结果重复
继续使用MEEP来作计算,这次将先会重复一下教科书的结果
“Photonic Crystals: Molding the Flow of Light “:P128 Figure5
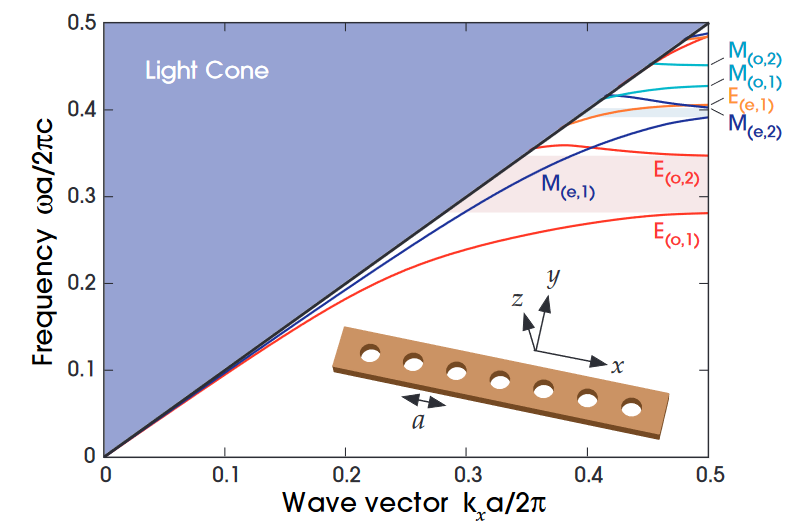
上图是要计算的结构,是一个纳米梁波导,其基本参数为:
- 周期设置为a=1
- 圆孔半径设置为r=0.25
- 宽度设置为w=1
- 高度设置为h=0.4
- 所用材料折射率为:3.4641
下面是MEEP的具体实现,首先是导入相应的包和设置基本参数
1 | #### import meep as mp |
然后开始设置MPB的物理模型1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19# 设置周期方向和大小,传播方向是周期的,设置为1,其他方向设置为4个周期大小,相应边界条件是不是为0?
geometry_lattice = mp.Lattice(size=mp.Vector3(1,4,4))
# 设置几何结构
geometry = [ mp.Block(center=mp.Vector3(), size=mp.Vector3(mp.inf,w,h), material=Si),
mp.Cylinder(center=mp.Vector3(), radius=r, height=mp.inf, material=mp.air) ]
# 沿着传播方向改变波矢
num_k = 20
k_points = mp.interpolate(num_k, [mp.Vector3(0,0,0), mp.Vector3(0.5,0,0)])
# 五个本征值
num_bands = 5
# 初始化modesolver
ms = mpb.ModeSolver(geometry_lattice=geometry_lattice,
geometry=geometry,
k_points=k_points,
resolution=resolution,
num_bands=num_bands)
根据对称性的不同,可以计算出不同的模式,我们这里可以计算模式是关于y奇对称,z偶对称
1 | # 限制我们关注的模式是关于y奇对称,z偶对称 |
最后取出相应的模式进行绘图1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17import matplotlib.pyplot as plt
import numpy as np
freqs = ms.all_freqs
gaps = ms.gap_list
kx=np.linspace(0,0.5,num_k+2)
fig=plt.figure()
for l in range(num_bands):
plt.plot(kx,freqs[:,l])
plt.plot(kx,kx,'k')
plt.ylim([0,0.5])
plt.grid('on')
plt.ylabel('$\omega a/(2\pi c)$')
plt.xlabel('$k_{x} a/(2\pi)$')
下图是计算的能带图,可以看到,与教科书的(M(e,1),M(e,2))是有出入的,我尝试过优化resolution,但是和教科书一直有差距,不知道是什么原因。。。
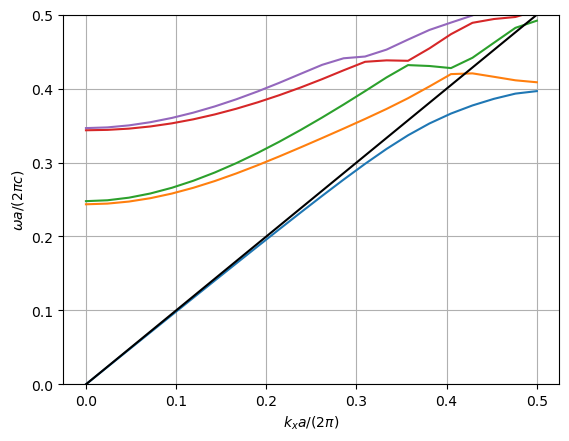
simpetuscloud例子重复
然后是重复simpetuscloud的一个例子,不知道什么原因,这个网页已经挂了
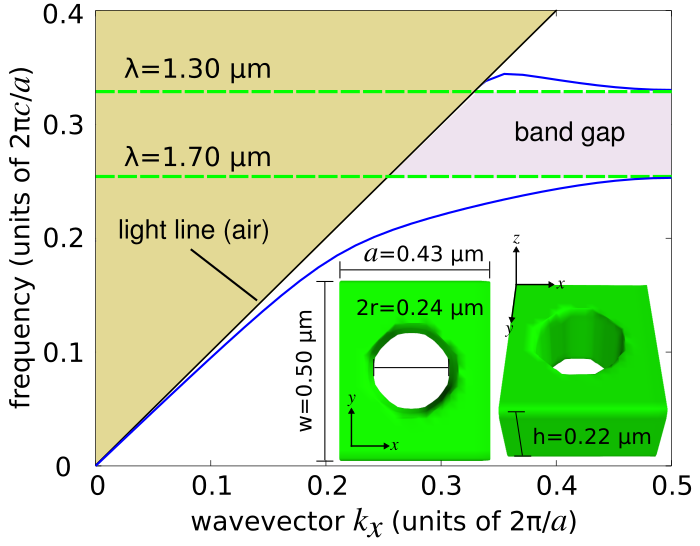
如上图所示是要重复的结构以及能带,基本设置方法和计算方法和第一个例子类似,只是结构有区别,代码不在这里展示了,直接给出计算结果
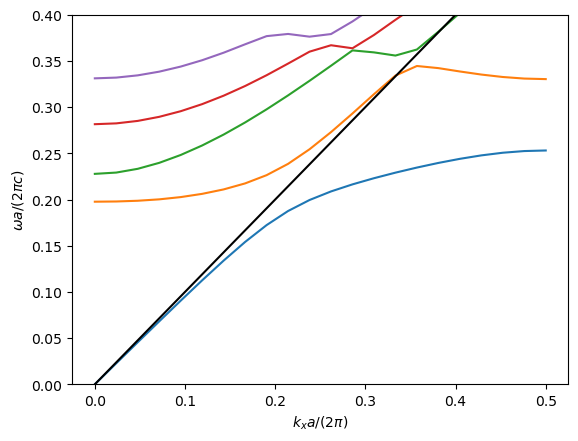
也可以导出相应的电场分布:
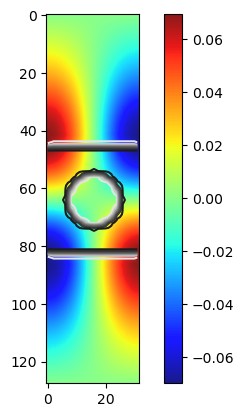
源代码
以上的两个粒子,源代码可以从我的Github仓库获取: