Meep

介绍

因为实验室需要，我的研究生生涯相当一部分就是在计算这个耦合效率，偶极子放在波导附近时，其一部分能量会耦合到波导中去，偶极子可以是任意的荧光分子、量子点等，我们希望提高这个耦合效率，其定义为耦合到波导部分的功率比上总的辐射功率

其中$p{guide}是偶极子耦合到波导的功率，需要在传播方向上将总场与波导模式场进行投影得到，而p{total}$则是偶极子总的辐射功率，需要计算包裹偶极子的一个封闭面上的坡印廷矢量的积分。这是最一般最有效的方法，其实还有基于模式分析的半解析方法来计算，我这里就不在详细讨论，本笔记目的只是为了计算出正确的耦合效率。

波导模式求解

这次的结构要复杂一些，如下图所示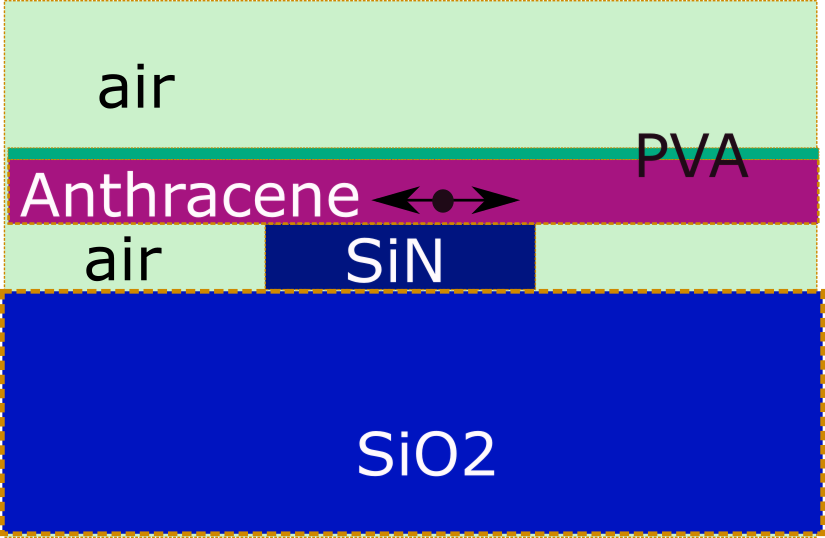

我们还是需要先求解一下对应的波导模式，和上篇笔记的做法一样，只是结构更加复杂了，设置结构的代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import meep as mp
from meep import mpb
import numpy as np
from matplotlib import pyplot as plt

omega = 1/0.78
# index of material
index_SiN=2.02
index_SiO2=1.46
index_PVA=1.5
index_An=1.8
# The size of the guide
width=0.65
height=0.25

height_An=0.2
height_PVA=0.03

# The size of simulation domain
width_cal=2.5
length_cal=2.5
height_cal=2.5

# Thinkness of PML
t_pml=0.4

# The size of box to obatin the dipole power
size_x=0.3
size_y=0.3
size_z=0.3

# The position of dipole
pos_x=0
pos_y=0
pos_z=height+0.005

resolution=50
numx=int(width_cal*resolution)
numy=int(height_cal*resolution)
x_list=np.linspace(-width_cal/2,width_cal/2,numx)
y_list=np.linspace(-height_cal/2,height_cal/2,numy)
x_grid,y_grid=np.meshgrid(x_list,y_list)
# %%
cell_size = mp.Vector3(length_cal,width_cal,height_cal)

pml_layers = [mp.Absorber(thickness=t_pml,direction=mp.Y),
                   mp.PML(thickness=t_pml,direction=mp.Z),
                   mp.PML(thickness=t_pml,direction=mp.X)]

# Y dipole 
source = [mp.Source(mp.ContinuousSource(frequency= omega), 
            component = mp.Ex, center=mp.Vector3(0, 0, 0.255) )]

geometry = [mp.Block(material=mp.Medium(epsilon=index_SiN**2), 
                     size=mp.Vector3(mp.inf,width, height),
                     center=mp.Vector3(0, 0, height/2)),

            mp.Block(material=mp.Medium(epsilon=index_SiO2**2),
                     size=mp.Vector3(mp.inf,mp.inf, height_cal/2),
                     center=mp.Vector3(0, 0, -height_cal/4)),

            mp.Block(material=mp.Medium(epsilon=index_An**2),
                     size=mp.Vector3(mp.inf,mp.inf, height_An),
                     center=mp.Vector3(0, 0, height+height_An/2)),
            mp.Block(material=mp.Medium(epsilon=index_PVA**2),
                     size=mp.Vector3(mp.inf,mp.inf, height_PVA),
                     center=mp.Vector3(0, 0, height+height_An+height_PVA/2))
                     ]

然后是计算波导模式和绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
geometry_lattice = mp.Lattice(size=mp.Vector3(0, width_cal, height_cal))
num_modes = 1
ms = mpb.ModeSolver(
    geometry_lattice = geometry_lattice,
    geometry         = geometry,
    resolution       = resolution,
    num_bands        = num_modes)
# ms.init_sim()
# %%
E = []
store_fields = lambda ms_temp, mode: E.append(ms_temp.get_efield(which_band=mode,bloch_phase=False))    

mode=1
k = ms.find_k(
    mp.NO_PARITY, # p
    omega, # omega
    mode, # band_min
    mode, # band_max
    mp.Vector3(1,0,0), # korig_and_kdir
    1e-4, # tol
    omega * 2, # kmag_guess
    omega * 0.1, # kmag_min
    omega * 4, # kmag_max
    store_fields # band_funcs
    )
# %%
neff=k[0]/omega
eps = ms.get_epsilon()
eps_arr=np.transpose(np.array(eps))

# %%
plt.figure(figsize=(12,4))
# Plot the E fields
mode=0
Ex=np.squeeze(E[mode][:,:,0,0]).transpose()
Ey=np.squeeze(E[mode][:,:,0,1]).transpose()
Ez=np.squeeze(E[mode][:,:,0,2]).transpose()

print('Current band: {}'.format(mode+1))
plt.subplot(1,3,1)
# plt.pcolormesh(x_grid,y_grid,eps.transpose(), cmap='binary')
plt.pcolormesh(x_grid,y_grid,np.abs(Ex), cmap='jet', alpha=0.9)
plt.axis('off')
plt.title('Ex')
plt.subplot(1,3,2)
# plt.pcolormesh(x_grid,y_grid,eps.transpose(), cmap='binary')
plt.pcolormesh(x_grid,y_grid,np.abs(Ey), cmap='jet', alpha=0.9)
plt.axis('off')
plt.title('Ey')
plt.subplot(1,3,3)
# plt.pcolormesh(x_grid,y_grid,eps.transpose(), cmap='binary')
plt.pcolormesh(x_grid,y_grid,np.abs(Ez), cmap='jet', alpha=0.9)
plt.axis('off')
plt.title('Ez')
plt.tight_layout()
plt.show()
plt.savefig('SimulatedField_onChip.png')

其模场分布如下

其折射率平方的分布绘制出来，便于我们进一步检查结构是否准确

1
2
3
4
5
fig1=plt.figure()
plt.pcolormesh(x_grid,y_grid,eps_arr,  cmap='jet')
plt.colorbar()
plt.savefig('StructuresonChip.png')
plt.show()

其分布如下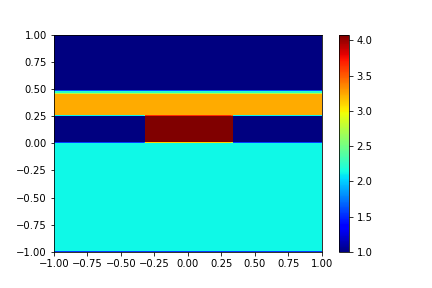

因此我们的结构设置是没有问题的。

求解耦合效率

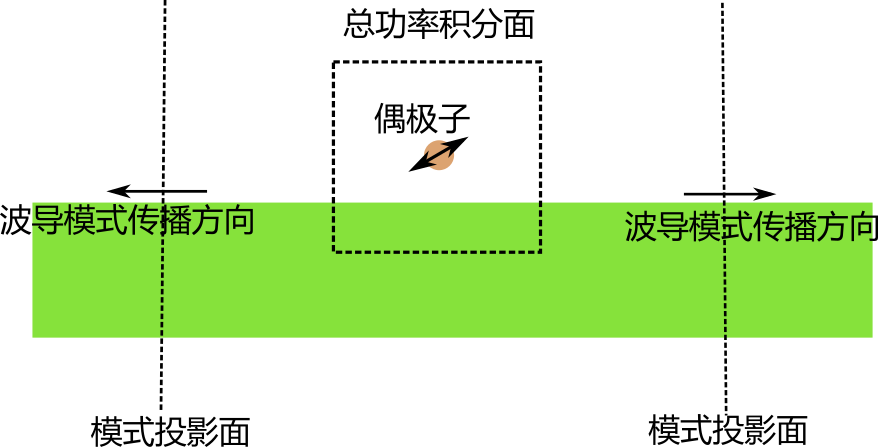
我们需要设置一个封闭的面包裹住偶极子，将表面的功率密度积分，得到总功率，还需要设置两个模式投影，其实只需要一个，因为结构是对称的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
sim = mp.Simulation(resolution=resolution,

 cell_size=cell_size,

 boundary_layers=pml_layers,

 geometry=geometry,

 sources=source,

 eps_averaging= False,

 Courant = 0.5)

 # 模式投影面设置

box_1 = sim.add_mode_monitor(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(0.2, 0, 0),

 size=mp.Vector3(0,width_cal,height_cal))) 

box_2 = sim.add_mode_monitor(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(-0.2, 0, 0),

 size=mp.Vector3(0,width_cal,height_cal))) 

  

# 总积分面设置

box_x1 = sim.add_flux(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(pos_x-size_x/2,pos_y,pos_z),size=mp.Vector3(0,size_y,size_z)))

box_x2 = sim.add_flux(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(pos_x+size_x/2,pos_y,pos_z),size=mp.Vector3(0,size_y,size_z)))

  

box_y1 = sim.add_flux(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(pos_x,pos_y-size_y/2,pos_z),size=mp.Vector3(size_x,0,size_z)))

box_y2 = sim.add_flux(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(pos_x,pos_y+size_y/2,pos_z),size=mp.Vector3(size_x,0,size_z)))

  

box_z1 = sim.add_flux(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(pos_x,pos_y,pos_z-size_z/2),size=mp.Vector3(size_x,size_y,0)))

box_z2 = sim.add_flux(omega, 0, 1,

mp.FluxRegion(center=mp.Vector3(pos_x,pos_y,pos_z+size_z/2),size=mp.Vector3(size_x,size_y,0)))

  

# %%

然后就可以计算然后输出结果了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# sim.run(until_after_sources=

# mp.stop_when_fields_decayed(20, mp.Ey, pt, 1e-3))

# sim.run(until_after_sources=20)

sim.run(until=20)

# %%

x1 = mp.get_fluxes(box_x1)

x2 = mp.get_fluxes(box_x2)

y1 = mp.get_fluxes(box_y1)

y2 = mp.get_fluxes(box_y2)

z1 = mp.get_fluxes(box_z1)

z2 = mp.get_fluxes(box_z2)

  

mode1 = sim.get_eigenmode_coefficients(box_1,

 [1], eig_parity=mp.NO_PARITY)

mode2 = sim.get_eigenmode_coefficients(box_2,

 [1], eig_parity=mp.NO_PARITY)

  

# %%

ptotal = -x1[0]+x2[0]-y1[0]+y2[0]-z1[0]+z2[0]

pmode_1 = abs(mode1.alpha[0,0,0])**2

pmode_2 = abs(mode2.alpha[0,0,1])**2

effic_1=pmode_1/ptotal

effic_2=pmode_2/ptotal

neff1 = mode1.kdom[0].x/omega

neff2 = mode2.kdom[0].x/omega

print(neff1)

print(neff2)

print("efficency to position direction:, {} ".format(effic_1))

print("efficency to negative direction:, {} ".format(effic_2))

收敛性测试

为了检查收敛性，我还改变了不同的分辨率（resolution），看结果是否准确，
代码地址
其结果如下

可以看见其实只需要50的分辨率就可以了，后面结果变化的很小。

与Lumerical和FDTD对比

另外我又扫描了偶极子的竖直高度和Lumerical FDTD以及COMSOL的解析结果对比，代码地址

其结果如下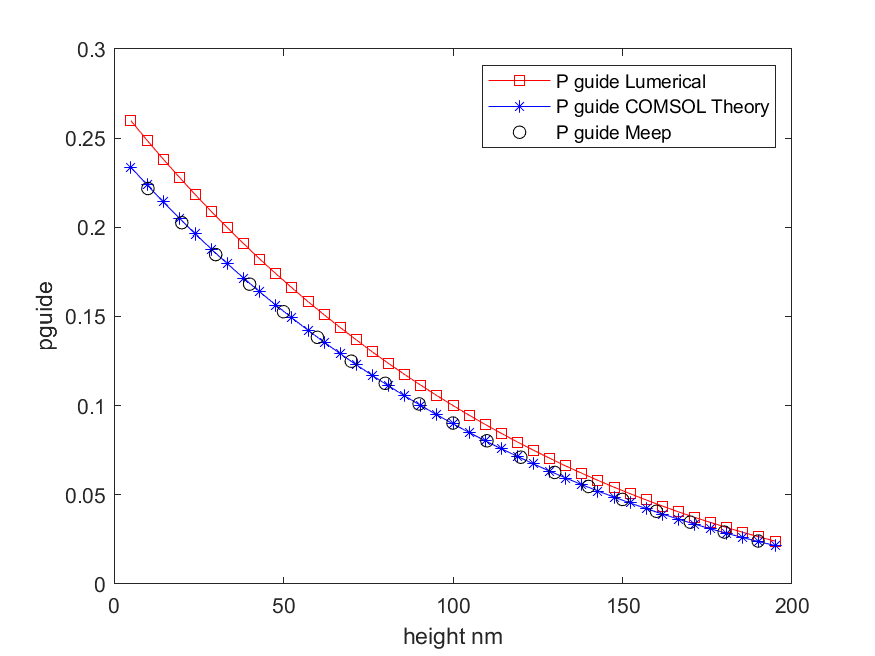


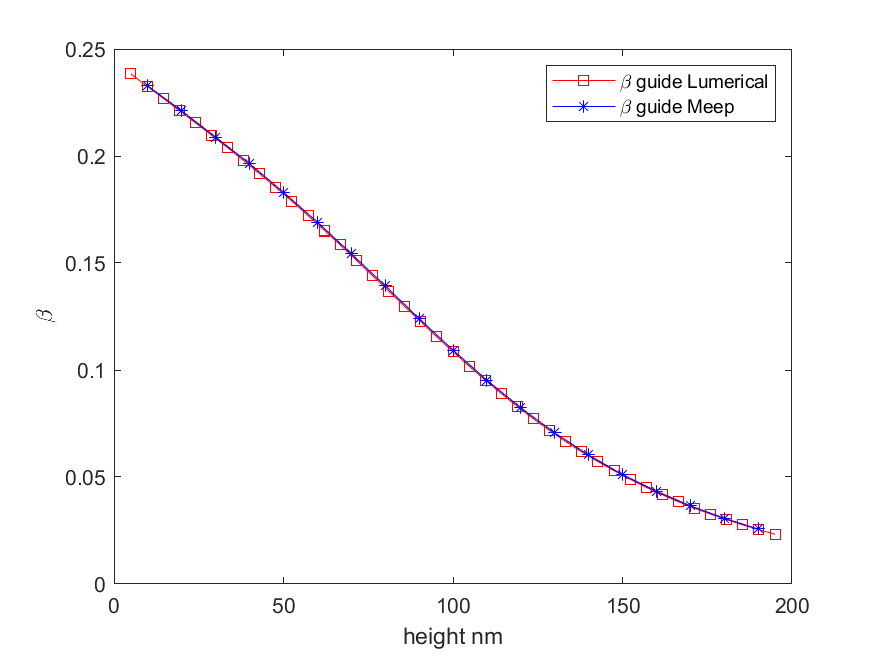
可以看见Meep的Pguide的结果与COMSOL理论符合的非常好，与LumeircalFDTDSlutions不那么好，这与LumeircalFDTDSlutions归一化不好有关，而耦合效率吧则是完全对上的。

以上就是计算的全过程了。如果对你有帮助记得点赞~