Meep

目的

安装完Meep之后一直很少用它来做具体的计算，因为COMSOL和Lumerical FDTD Solutions确实有图形界面非常好用，最近想要计算偶极子耦合到直波导的耦合效率，用COMSOL计算三维结构需要较大的内存，用FDTD的时候服务器没有图形界面，扫描设置很不方便，这时候决定好好打磨一下Meep以为我所用。我的思路是：

学会用Meep计算光波导模式并和COMSOL对上
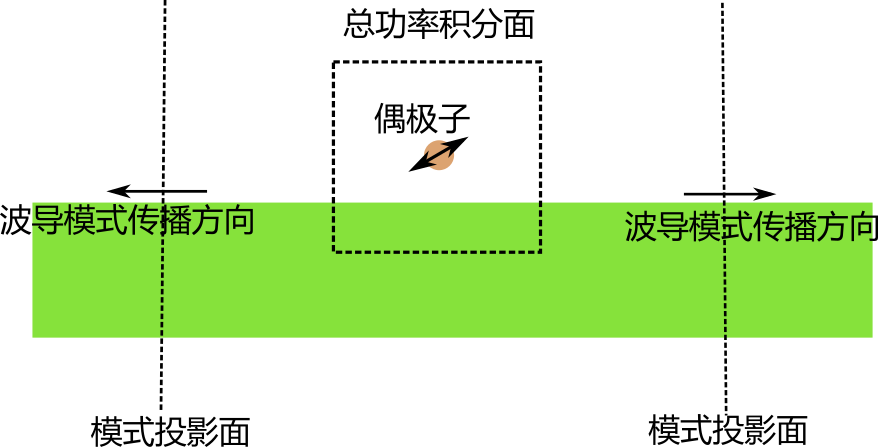
学会用Meep设置偶极子的源计算并计算器耦合到波导模式的功率

今天笔记主要讲的是第一步。

那里可以学习？

Meep如果直接去浏览官方文档还是比较低效的，最好是可以直接从例子中学习，有不懂再去看。我也希望我把我的例子写出来可以帮助大家快速上手，用Meep计算波导模式有两个方法，我是各种浏览github的问题区域知道的，里面别人分享了很多的源代码。比如别人问为啥MPB和Meep计算的结果不一样，我就可以知道有两个方法计算波导模式：

issues893
另外具体的设置步骤还参考了这个讨论
issues851
还有一个网站有非常多的例子，我觉得需要一级推荐的
[simpetuscloud]（http://www.simpetuscloud.com/projects.html#mpb_waveguide）
如果要查询一斜函数的用法，可以查询这个页面
[Python_User_Interface](https://meep.readthedocs.io/en/latest/Python_User_Interface/）

总之就是多看别人的例子再去查询函数用法，我觉得是最快的。

实现过程

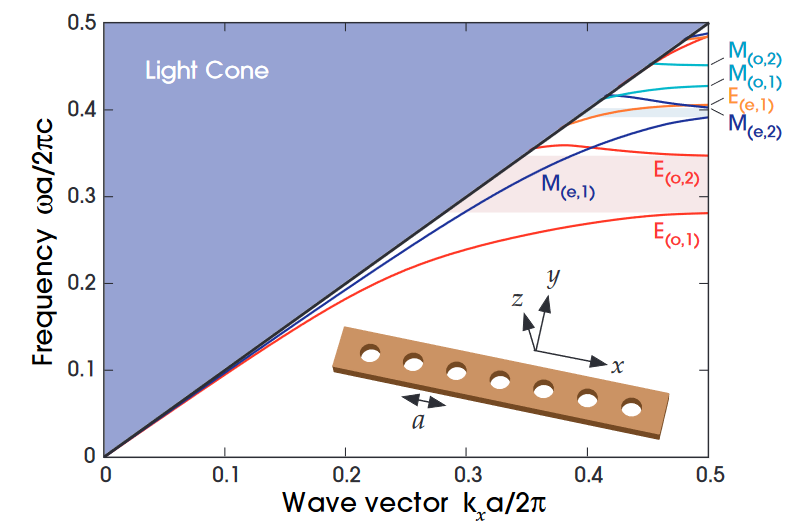
我现在要计算的是，宽度为650nm，高度为250nm的SiN波导在波长为780nm处的波导模式。其结构如下

MPB实现

首先是插入一下包和设置基本的结构参数

import meep as mp
from meep import mpb
import numpy as np
from matplotlib import pyplot as plt

# Then the wavelength
omega = 1/0.78
material_SiN=mp.Medium(index=2.02)
width_guide=0.65
height_guide=0.25

接下来就是要初始化处几何结构(geometry)，格点个数（resolution,每1um多少个）,我们先用MPB实现，这样我们还需要初始化三维原胞的结构，如下

resolution=200
size_cal_y=2
size_cal_z=2

geometry = [mp.Block(material=material_SiN, 
                     size=mp.Vector3(mp.inf,width_guide, height_guide),
                     center=mp.Vector3(0, 0, height_guide/2))]
geometry_lattice = mp.Lattice(size=mp.Vector3(0, size_cal_y, size_cal_z))

我们的波导方向沿着X，只是为了计算模式，厚度设置为0，为一个二维问题。然后是设置我们要计算几个模式以及初始化计算对象

num_modes = 4

ms = mpb.ModeSolver(
    geometry_lattice = geometry_lattice,
    geometry         = geometry,
    resolution       = resolution,
    num_bands        = num_modes
)

参数的详细设置可以参见源文档。接下来我们需要设置一个函数来讲每次计算的模式的场分布取出，这是通过上面的链接issues851学到的，即需要设置

1 2	E = [] store_fields = lambda ms_temp, mode: E.append(ms_temp.get_efield(which_band=mode,bloch_phase=False))

然后就可以计算了

k = ms.find_k(
    mp.NO_PARITY,
    omega, # omega
    1, # band_min
    num_modes, # band_max
    mp.Vector3(1,0,0), # korig_and_kdir
    1e-4, # tol
    omega * 2, # kmag_guess
    omega * 0.1, # kmag_min
    omega * 2, # kmag_max
    store_fields, # band_funcs
)
neff=k[0]/omega # 有效折射率
eps = ms.get_epsilon() # 折射率分布
eps_arr=np.transpose(np.array(eps))

绘制结果

# %%
x_list=np.linspace(-size_cal_y/2,size_cal_y/2,resolution*2)
y_list=np.linspace(-size_cal_z/2,size_cal_z/2,resolution*2)
x_grid,y_grid=np.meshgrid(x_list,y_list)

plt.figure(figsize=(12,4))
# Plot the E fields
for mode in range(num_modes):
    Ex=np.squeeze(E[mode][:,:,0,1]).transpose()
    print('Current band: {}'.format(mode+1))
    plt.subplot(1,num_modes,1+mode)
    plt.pcolormesh(x_grid,y_grid,eps.transpose(), cmap='binary')
    plt.pcolormesh(x_grid,y_grid,np.abs(Ex), cmap='jet', alpha=0.9)
    plt.axis('off')
    st_title='Ex of mode '+str(mode+1)+' from MPB neff=' +str('%.2f' %(k[mode]/omega))
    plt.title(st_title)
plt.tight_layout()
plt.savefig('SimulatedFieldMPB.png')
plt.show()

上面分别绘制出来了四个模式的Ex分量的实部。

Meep实现

首先是插入一下包和设置基本的结构参数,和之前一样

import meep as mp
from meep import mpb
import numpy as np
from matplotlib import pyplot as plt

#Then the wavelength
omega = 1/0.78
material_SiN=mp.Medium(index=2.02)
width_guide=0.65
height_guide=0.25
resolution=200
size_cal_y=2
size_cal_z=2

geometry = [mp.Block(material=material_SiN, 
                     size=mp.Vector3(mp.inf,width_guide, height_guide),
                     center=mp.Vector3(0, 0, height_guide/2))]

不同的是接下来我们需要设置PML边界条件,并同样的初始化对象

num_modes = 4

dpml = 0.5
pml_layers = [mp.PML(dpml)]
sim = mp.Simulation(cell_size=mp.Vector3(0,size_cal_y+dpml*2,size_cal_z+dpml*2),
                    resolution=resolution,
                    geometry=geometry,
                    boundary_layers=pml_layers,)

sim.init_sim()
where = mp.Volume(center=mp.Vector3(), size=mp.Vector3(0,size_cal_y,size_cal_y))
direction = mp.X #波导方向
kpoint = mp.Vector3(1,0,0)

然后是计算，但是得提前准备好坐标，因为meep的函数get_eigenmode函数只能得到一个amplitude的方法，你可以通过该方法插值出场的数值，这个也是我仔细研究了一下函数的用法才发现的，所以算模式还是MPB吧

x_list=np.linspace(-size_cal_y/2,size_cal_y/2,resolution*2)
y_list=np.linspace(-size_cal_z/2,size_cal_z/2,resolution*2)
x_grid,y_grid=np.meshgrid(x_list,y_list)
pos_extract=mp.Vector3(np.ravel(x_grid)*0,np.ravel(x_grid),np.ravel(y_grid))
Ex_mp=np.zeros((resolution*2,resolution*2,num_modes),dtype=complex)
# Extract the field in a loop
num_modes=4
k_meep=np.zeros(num_modes)
for mode in range(num_modes):
    print('Simultion Mode'+str(mode+1))
    ed = sim.get_eigenmode(omega, direction, where, mode+1, kpoint, eig_vol=None, match_frequency=True, 
    parity=mp.NO_PARITY, resolution=resolution, eigensolver_tol=1e-12)
    k_meep[mode]=ed.k[0]
    for l in range(resolution*2):
        for m in range(resolution*2):
            Ex_mp[l,m,mode]=ed.amplitude(mp.Vector3(0,x_list[m],y_list[l]),1)

然后绘制结果

plt.figure(figsize=(14,4))
for mode in range(num_modes):
    print('Current band: {}'.format(mode+1))
    plt.subplot(1,num_modes,1+mode)
    plt.pcolormesh(x_grid,y_grid,np.abs(Ex_mp[:,:,mode]), cmap='jet', alpha=0.9)
    plt.axis('off')
    st_title='Ex of mode '+str(mode+1)+' from MEEP neff=' +str('%.2f' %(k_meep[mode]/omega))
    plt.title(st_title)
plt.tight_layout()
plt.savefig('SimulatedFieldMeep.png')
plt.show()

放在一起比较

plt.figure(figsize=(12,8))
for mode in range(num_modes):
    print('Current band: {}'.format(mode+1))
    plt.subplot(2,num_modes,1+mode)
    plt.pcolormesh(x_grid,y_grid,np.abs(Ex_mp[:,:,mode]), cmap='jet', alpha=0.9)
    plt.axis('off')
    st_title='Ex of mode '+str(mode+1)+' from MEEP neff=' +str('%.2f' %(k_meep[mode]/omega))
    plt.title(st_title)
for mode in range(num_modes):
    Ex=np.squeeze(E[mode][:,:,0,1]).transpose()
    print('Current band: {}'.format(mode+1))
    plt.subplot(2,num_modes,1+mode+num_modes)
    plt.pcolormesh(x_grid,y_grid,np.abs(Ex), cmap='jet', alpha=0.9)
    plt.axis('off')
    st_title='Ex of mode '+str(mode+1)+' from MPB neff=' +str('%.2f' %(k[mode]/omega))
    plt.title(st_title)

plt.tight_layout()
plt.savefig('SimulatedFieldCompare.png')
plt.show()