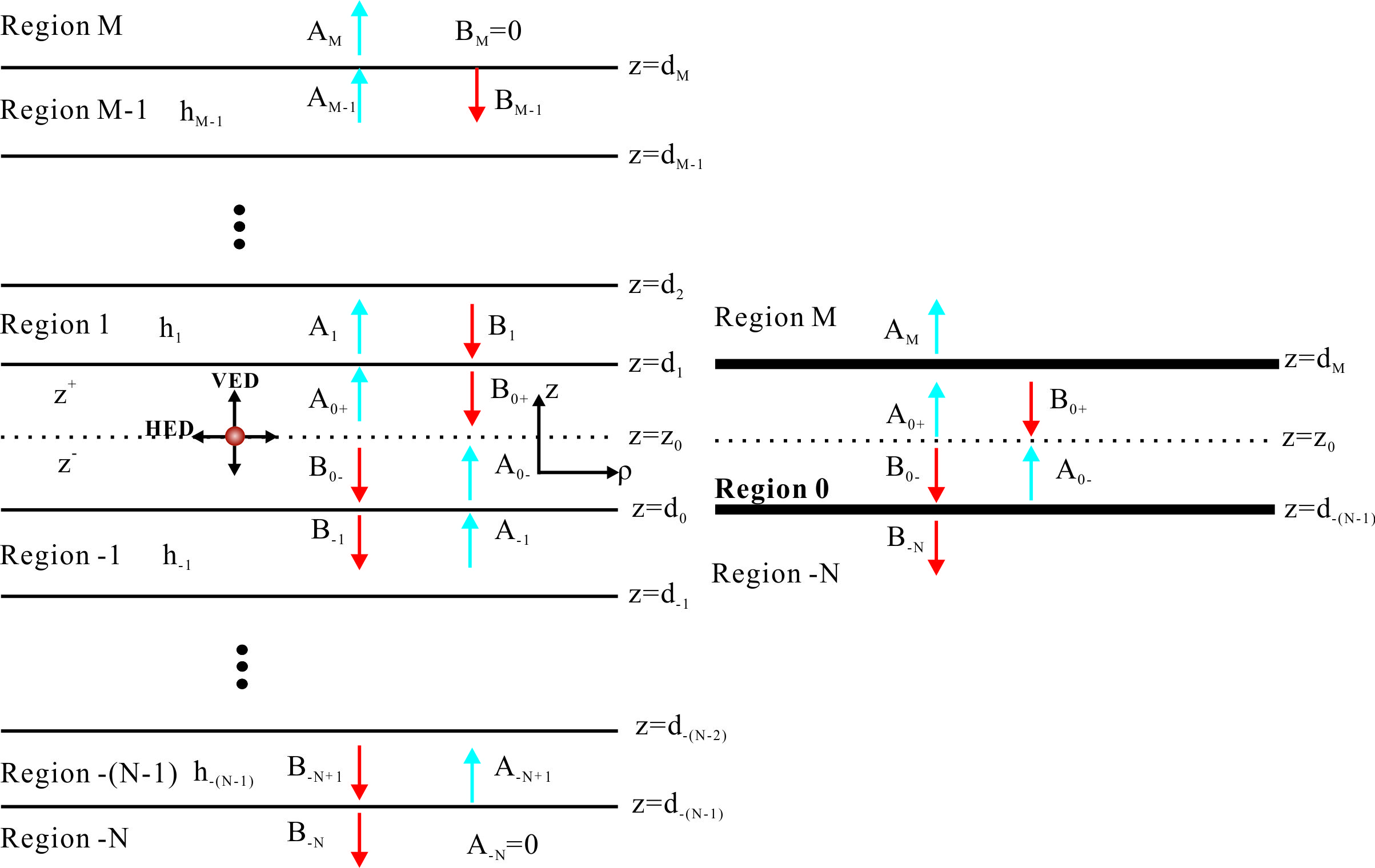
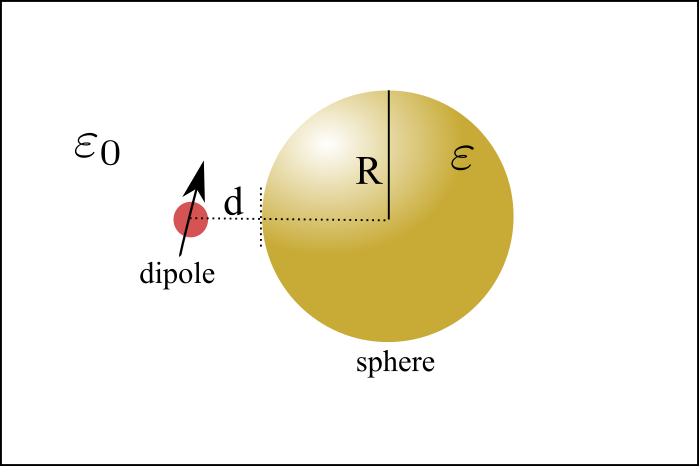
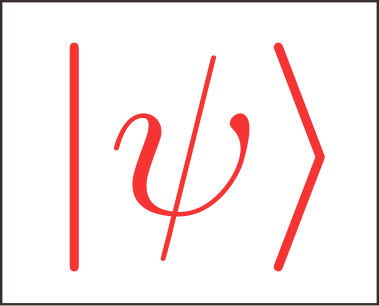Python #Dataprocessing
介绍
对于我个人而言,无论是用MATLAB,或者是python,我都没有系统的学习过。喜欢在网络上搜索一个别人的代码,拿来改一改,就直接用,不明白背后的机理。实际自己编程时候,不去网络上搜索就寸步难行。为了改变这种状况,我决定对于编程进行一些定期的专题总结。
python的numpy库可以很好的支持矩阵的一些运算,对于数值计算以及数据处理非常方便,但是自己在使用的过程中发现有很多特性需要着重总结一下,避免后续写程序的时候做一些无用功。本篇笔记主要是想详细讨论矩阵这一元素的基本操作以及可视化规律。首先应该插入对应的包。
1
2
| import numpy as np
import matplotlib.pyplot as plt
|
矩阵的初始化
矩阵初始化有好几种形式,也有一些特殊的函数来初始化,我们要分清矩阵的形状如何。是行矩阵还是列矩阵,首先是默认的初始化化行和列
1
2
| A=np.array([1,2,3])
print(A,A.shape)
|
1
2
| B=np.array([[1],[2],[3]])
print(B,B.shape)
|
上面两种不同的创建方式所形成的矩阵的形状是不一样的,如果直接输入“[1,2,3]”,则是一 个(3,)形状的矩阵,即是一个一维矩阵,第二个维度是没有的,用中括号括起来之后,则是(3,1)的矩阵,可以是一个二维矩阵,矩阵只有一列。关于“,”的用法还不是很熟悉。
接下来看如何定义一个二维矩阵
1
2
3
4
| C=np.array([[1,2,3],[4,5,6]])
print(C)
print(C.shape)
|
1
2
3
| [[1 2 3]
[4 5 6]]
(2, 3)
|
这种方法创建的矩阵,每一个中括号构成了矩阵的一行。,最终形状为(2,3),代表有两行三列。初始化矩阵还可以用一些特殊函数,和MATLAB一样,有”ones”,”zeros”,”eye”,”rand”,”identity”
1
2
3
| ones_mat=np.ones((2,3))
print('for ones')
print(ones_mat)
|
1
2
3
| for ones
[[1. 1. 1.]
[1. 1. 1.]]
|
1
2
3
| zeros_mat=np.zeros((2,3))
print('for zeros')
print(zeros_mat)
|
1
2
3
| for zeros
[[0. 0. 0.]
[0. 0. 0.]]
|
1
2
3
| eye_mat=np.eye(2,3)
print('for eys')
print(eye_mat)
|
1
2
3
| for eys
[[1. 0. 0.]
[0. 1. 0.]]
|
1
2
3
| identity_mat=np.identity(3)
print('for indentity')
print(identity_mat)
|
1
2
3
4
| for indentity
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
|
1
2
3
| rand_mat=np.random.rand(2,3)
print('for rand')
print(rand_mat)
|
1
2
3
| for rand
[[0.99397064 0.5067113 0.29838922]
[0.09256186 0.58608547 0.71958337]]
|
矩阵的索引与切片
我们非常常见的操作是选取矩阵的某一些元素,比如某一行,某一列,第几行到第几列等。还是以上面创建的矩阵为例子,我们要选取矩阵C的第二列的话
第二行的话
与MATLAB的用法一样,除了括号变为方括号,序数从0开始没有什么差别,接下里要选取C的前两列,MATLAB怎么选呢?
但是python却不一样,python的
只是第一列而已,我们可以验证
这是一个非常不同的点,我开始想当然认为与MATLAB一样,导致出现了一些错误。
网格矩阵
我们的一种操作是网格矩阵,因为需要再二维或者三维空间描述数据。在此之前,我需要介绍几个特殊的矩阵操作函数。首先是reshae函数
1
2
| C_reshape=np.reshape(C,6)
print(C_reshape)
|
我们不难发现,python是第一行第一列第一个元素、第二个元素…第二行第一个元素这样的顺序来访问数组元素。第二个函数是ravel函数
1
2
| C_ravel=np.ravel(C)
print(C_ravel)
|
结果也是一样。这好像于MATLAB是反的?即使这样,索引的第一个参数是第几行,第二个参数是第几列。
为了查看网格矩阵的产生,我们需要两个一维矩阵。
1
2
3
4
| x=np.linspace(0,5,6)
y=np.linspace(4,10,7)
print(x)
print(y)
|
1
2
| [0. 1. 2. 3. 4. 5.]
[ 4. 5. 6. 7. 8. 9. 10.]
|
我们来测试下两种不同的方式产生grid
1
| x1_grid,y1_grid=np.meshgrid(x,y)
|
1
2
3
4
5
6
7
| [[0. 1. 2. 3. 4. 5.]
[0. 1. 2. 3. 4. 5.]
[0. 1. 2. 3. 4. 5.]
[0. 1. 2. 3. 4. 5.]
[0. 1. 2. 3. 4. 5.]
[0. 1. 2. 3. 4. 5.]
[0. 1. 2. 3. 4. 5.]]
|
1
2
3
4
5
6
7
| [[ 4. 4. 4. 4. 4. 4.]
[ 5. 5. 5. 5. 5. 5.]
[ 6. 6. 6. 6. 6. 6.]
[ 7. 7. 7. 7. 7. 7.]
[ 8. 8. 8. 8. 8. 8.]
[ 9. 9. 9. 9. 9. 9.]
[10. 10. 10. 10. 10. 10.]]
|
对于函数,np.meshgrid(x,y),x的长度作为列数,y的长度作为行数,x作为特殊行复制变成x_grid,y作为特殊列复制变成有grid。
接下来分析更加复杂的网格,分析其性质。我们有首先创造三个一维矩阵
1
2
3
4
| m_1=np.linspace(0,9,49)
m_2=np.linspace(0,10,50)
m_3=np.linspace(0,11,51)
m1_grid,m2_grid,m3_grid=np.meshgrid(m_1,m_2,m_3)
|
1
| z_3d=np.cos(m1_grid)*(m2_grid)**2*np.sin(m3_grid)
|
1
2
3
4
5
6
7
8
| fig=plt.figure(figsize=(6.4*3,4.8))
plt.subplot(131)
plt.imshow(z_3d[:,:,15],cmap='jet')
plt.subplot(132)
plt.imshow(z_3d[:,0,:],cmap='jet')
plt.subplot(133)
plt.imshow(z_3d[15,:,:],cmap='jet')
plt.show()
|
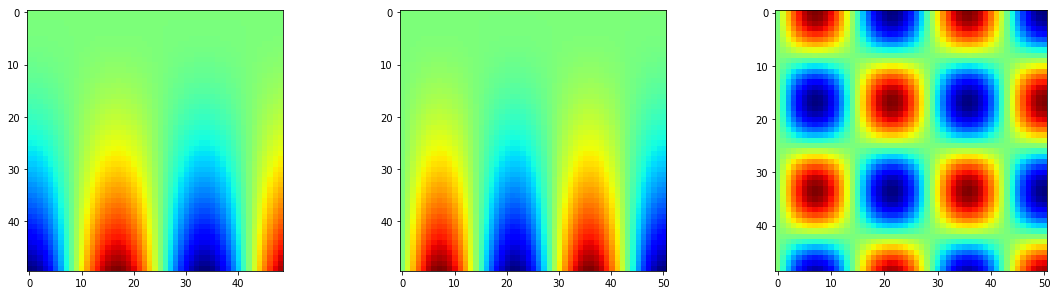
以上是一些矩阵的切片。我现在想的是在将上面的矩阵变成一维矩阵之后,如何reshape回来?即
1
2
3
4
5
6
7
8
9
10
| z_1d=np.cos(np.ravel(m1_grid))*(np.ravel(m2_grid))**2*np.sin(np.ravel(m3_grid))
z_3d_re=np.reshape(z_1d,(50,49,51))
fig=plt.figure(figsize=(6.4*3,4.8))
plt.subplot(131)
plt.imshow(z_3d_re[:,:,15],cmap='jet')
plt.subplot(132)
plt.imshow(z_3d_re[:,0,:],cmap='jet')
plt.subplot(133)
plt.imshow(z_3d_re[15,:,:],cmap='jet')
plt.show()
|
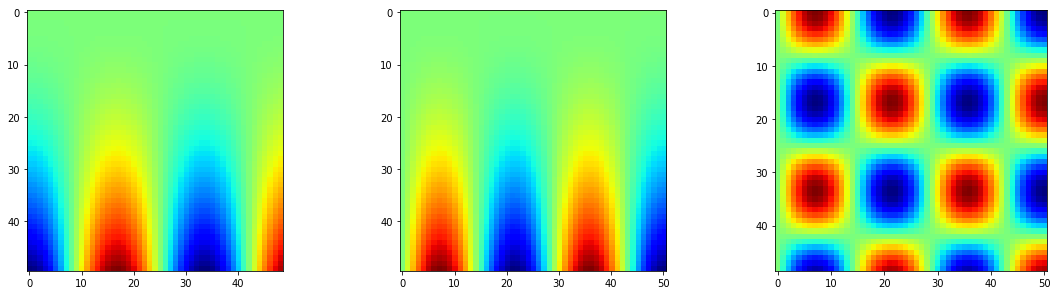
还是可以回来的,因此原来是什么样子,还是可以变回来。
绘图函数
另外需要注意的是绘图函数对于矩阵的操作。我们有一个二维矩阵,绘图之后,觉得与自己想的不符合,就转置一下,这样很容易浪费时间,因此我希望在此总结下。首先是用前面的矩阵创造一个二维分布数组。
1
2
3
4
| x2=np.linspace(-2,2,100)
y2=np.linspace(-2,2,100)
x2_grid,y2_grid=np.meshgrid(x2,y2)
z_color=(x2_grid**2+y2_grid**2)*np.sin(x2_grid)
|
1
2
3
| fig1=plt.figure()
plt.imshow(z_color,cmap='jet')
plt.show()
|
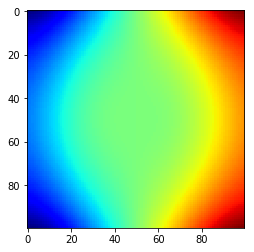
上面是将行作为横序数坐标,列序数作为纵坐标。而其他的函数呢?
1
2
3
4
5
6
| fig2=plt.figure(figsize=(13,4.8))
plt.subplot(121)
plt.pcolormesh(z_color,cmap='jet')
plt.subplot(122)
plt.pcolormesh(x2_grid,y2_grid,z_color,cmap='jet')
plt.show()
|
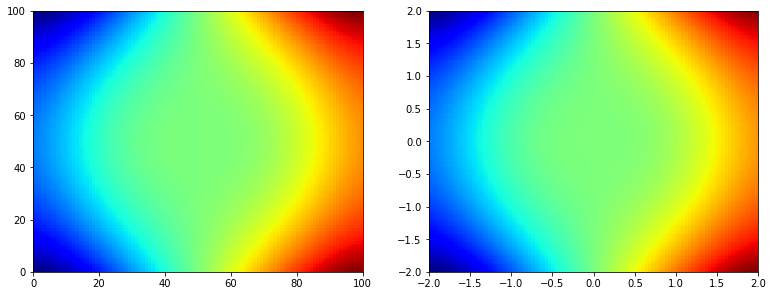
对于矩阵的形状不变,但是pcolormesh与imshow再x,y坐标的开始方面是不一样的。imshow的y轴从上至下是正方向,而x轴从左至右是正方向。pcolormeh在y轴上是反的,更加符合通常的思路。这一点要注意。这细枝末节,很容易造成错误。
高纬度矩阵的转置
还想提到的是高纬度矩阵的转置,有时候我们有一个三维的数据,我们绘图时候希望某一个特殊的轴作为z轴、x轴等,这就需要我们对三维矩阵在三维空间翻转。需要用到转置函数,需要用到的函数时transpose函数,其用法为
1
| numpy.transpose(a, axes=None)
|
axes是轴的序数,默认顺序是0,1,2,….,如果我们要交换某个矩阵,只需要更改顺序即可,下面是使用实例
1
2
| z_3d_1=np.transpose(z_3d,(1,0,2))
print(z_3d_1.shape)
|
所以用法一目了然.
注意矩阵转置时,与MATLAB有本质的不同,MATLAB是从列开始的,而python是通过行来检索的。