Data Visualization Via MATLAB (3 dimensional data)
MATLAB #Plot
Data Visualization Via MATLAB (3 dimensional data)
The three dimensinal data are composed of
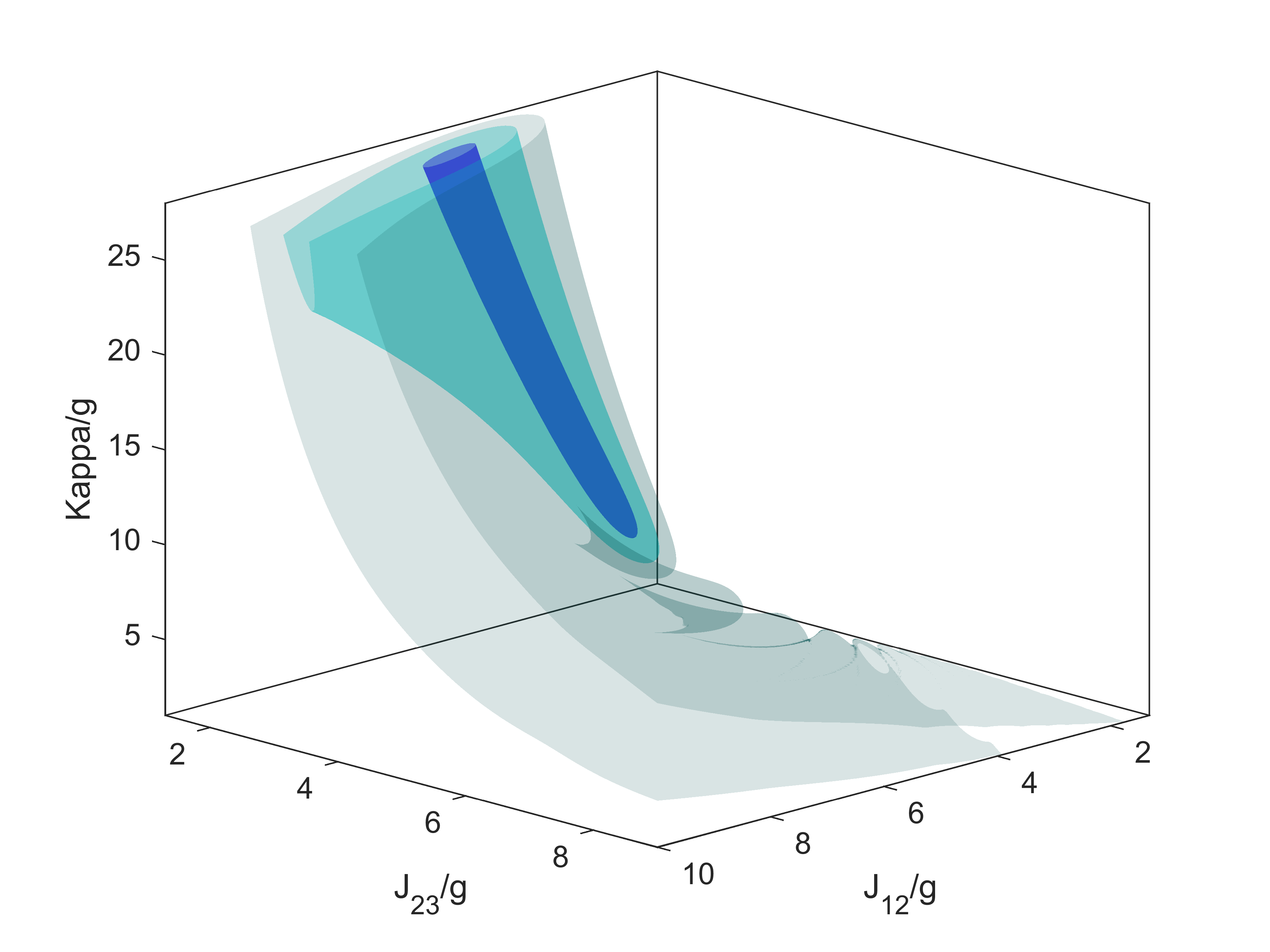
3d Contour Surface Plots
We should extract the contour data via the function isosurface. Though I have completed the figure, I can’t understand the reason. I will give issulation later.
1 | % As a study of 3D data visualization using MATLAB |
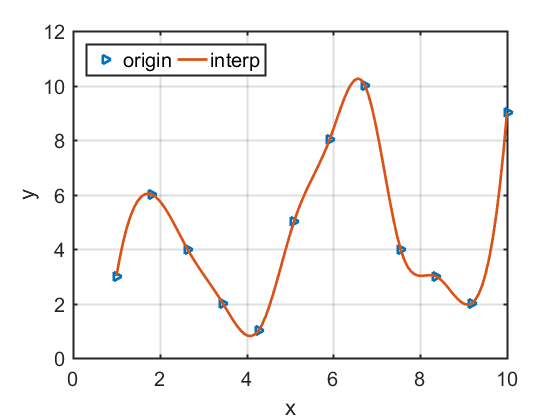
The generated plot are as follows
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
Comment