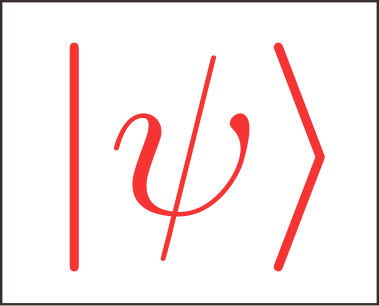如何正确使用非正交基矢展开某个矢量

物理

问题来源

最近在用非正交基矢处理一些问题，发现我之前的认知比较荒谬，所以写下这个笔记记录一下。

对于某个态 ，假设其可以写成三个归一化态基矢的叠加，且需 $|\psi1\rangle, |\psi_2\rangle|\psi_3\rangle|\psi{1,2}\rangle$ 都正交

$$|\psi\rangle = \alpha_1 |\psi_1\rangle + \alpha_2 |\psi_2\rangle + \alpha_3 |\psi_3\rangle \tag{1}$$

对于正交的基石，其系数通过基矢和 的内积获得

$$\alpha_n = \langle \psi_n | \psi \rangle \tag{2}$$

我们只关注编号为 1,2 基矢空间的向量长度，因此我们理论上可以定义一个新的向量

$$|\psi_{1,2}\rangle = \alpha_1 |\psi_1\rangle + \alpha_2 |\psi_2\rangle \tag{3}$$ $$|\psi\rangle = |\psi_{1,2}\rangle + \langle \psi | \psi_3 \rangle |\psi_3\rangle \tag{4}$$

而 的长度，可以直接由内积来计算：

$$\langle \psi_{1,2} | \psi_{1,2} \rangle = \alpha_1 \alpha_1^* \langle \psi_1|\psi_1 \rangle + \alpha_2 \alpha_2^* \langle \psi_2|\psi_2 \rangle + \alpha_1 \alpha_2^* \langle \psi_2|\psi_1 \rangle + \alpha_2 \alpha_1^* \langle \psi_1|\psi_2 \rangle \tag{5}$$

理论上也可以通过计算原始基矢和目标基矢的内积获得？就有两种不同的写法，第一种，直接展开，于上面的结果一样：

$$\langle \psi | \psi_{1,2} \rangle = \langle \alpha_1 \psi_1 + \alpha_2 \psi_2 + \alpha_3 \psi_3 | (\alpha_1 \psi_1 + \alpha_2 \psi_2) \rangle$$ $$= \alpha_1^* \alpha_1 \langle \psi_1|\psi_1 \rangle + \alpha_2^* \alpha_2 \langle \psi_2|\psi_2 \rangle + \alpha_3^* \alpha_1 \langle \psi_3|\psi_1 \rangle + \alpha_3^* \alpha_2 \langle \psi_3|\psi_2 \rangle + \alpha_1^* \alpha_2 \langle \psi_1|\psi_2 \rangle + \alpha_2^* \alpha_1 \langle \psi_2|\psi_1 \rangle \tag{6}$$

但是假设我们直接考虑内积呢？

$$\langle \psi | \psi_{1,2} \rangle = \alpha_1 \langle \psi|\psi_1 \rangle + \alpha_2 \langle \psi|\psi_2 \rangle = \alpha_1 \alpha_1^* + \alpha_2 \alpha_2^* \tag{7}$$

所以为什么二者之间的结果会有区别呢？是那一部出了问题呢？

问题原因

在正交归一基下，任意向量 都可以写成

$$|\phi\rangle = \sum_i \langle \psi_i | \phi \rangle \, |\psi_i\rangle .$$

但是，当基矢 不正交时，如果仍然直接取展开系数为 ，就会出现错误。

正确方法

1. 计算内积向量

   $$c_i = \langle \psi_i | \phi \rangle .$$

   得到向量 。

2. 构造 Gram 矩阵

   $$G_{ij} = \langle \psi_i | \psi_j \rangle .$$

   这是非正交基下的“度量矩阵”。

3. 求解展开系数
   需要解方程：

   $$G \, \boldsymbol{\alpha} = \mathbf{c} ,$$

   即

   $$\boldsymbol{\alpha} = G^{-1}\mathbf{c} .$$

   这样得到的 才是 在非正交基下的展开系数。

示例演算

设

1. 内积： $$c = \begin{pmatrix} \langle \psi_1 | \phi \rangle \\ \langle \psi_2 | \phi \rangle \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}.$$

2. Gram 矩阵：

   $$G = \begin{pmatrix} \langle \psi_1|\psi_1 \rangle & \langle \psi_1|\psi_2 \rangle \\ \langle \psi_2|\psi_1 \rangle & \langle \psi_2|\psi_2 \rangle \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix}.$$

3. 正确系数：

   $$\boldsymbol{\alpha} = G^{-1} c = \begin{pmatrix} 1 \\ 1 \end{pmatrix}.$$

   因此：

   $$|\phi\rangle = 1 \cdot |\psi_1\rangle + 1 \cdot |\psi_2\rangle .$$

   验证结果：，完全正确。

4. 如果错误地取 ，则得到：

   $$|\phi'\rangle = 2|\psi_1\rangle + 3|\psi_2\rangle = (5,3),$$

   与原向量偏差很大。

总结

• 正交基：展开系数直接是内积 。
• 非正交基：必须先构造 Gram 矩阵 ，再解方程 。
• 否则，得到的展开会出现系统性错误。