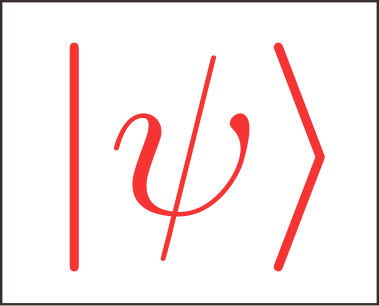量子计算与量子信息(二)量子隐形传态
Quantum #Optics
介绍
量子隐形传态是一个非常经典的利用纠缠来远距离传输量子态的方式,该方案需要我们首先具有一对纠缠的粒子(如光子),该方案在1993年被Bernet教授等人提出,并很快得到了实验上的验证,这篇笔记主要是想讲清楚该方案的原理以及实验方案。
EPR对
EPR无论是对于量子力学的发展还是对于量子信息的发展都至关重要。1935年Einstein, Podolsky, 和Rosen 提出了一个假想实验认为纠缠的粒子似乎会发生超距作用从而来否定量子力学的一些观点。EPR对即两个纠缠的粒子,可以是不同的物理量之间发生纠缠,物理量也可以分为连续变量和离散变量两种,离散变量描述相对简单,可以先用该变量说明:
非连续变量的表述
我们假设有两个纠缠的粒子比如电子,其自旋的方向更好是相反的,且满足守恒律,即一个如果自旋向上,那么一个就是自旋向下,可以将该粒子态表示为
如果将两个粒子放的非常远,此时测量粒子1,有可能自旋向上,也有可能自旋向下。但是一旦粒子1测量完毕,那么粒子2的状态也就跟着确定了。此时发生了超距作用!对于该超距作用,波尔认为,我们在测量之前,不存在所谓的两个粒子,只有测量之后,才具有实实在在的粒子。不过对于该EPR实验,我曾经有两点疑惑:
- 这不是发生了超光速作用吗?
其实不是的,因为粒子1测量了之后,只有通过经典手段将结果报告给粒子2的测量者,信息才算传递成功,所以信息并没有超光速。 - 这和我们闭着眼睛从一个盒子拿出一个红色、蓝色的球,然后如果一个是红色,那么另外一个就是蓝色,有何区别?
其实是有区别的,一个是叠加态,一个是个宏观混合的概率性事件。我们可以对两个纠缠的电子进行操作变成其他的方向纠缠的电子对,但是纠缠仍然存在。对于两个不同颜色的球来说,我将这边的球涂成淡蓝色不会让那边的球变成淡红色!
连续变量的表述
最开始在1935年,爱因斯坦他们表述的确实动量、坐标表象下的纠缠。
即两个的坐标是完全纠缠的,不过这个表示是不可归一化的,也是不物理的,不过我们可以认为其是对于某修分布的一些极限情况,比如高斯函数非常窄,我们就可以认为是一个
非连续变量表述的隐形传态
接下来我来介绍大家非常熟悉的非连续变量的隐形传态。我们假设Alice和Bob相距比较远,而且手中都具有一个EPR对中的一个粒子。Bell态作为纠缠最大的态有四个
假设由粒子A、B组成的EPR对表示为(其中的一个)
另外Alice手中还有一个态$|\psi{0}\rangle
用“0”表示这是初始态,接下来将Alice手中的态展开为贝尔态来看,需要用以下关系替换
因此
即如果我们此时在Bell基下测量,就会有四种结果,知道了结果之后,我们就知道Bob手中的态变成了什么,就可以相应的对手中的态做变换即可。例如我们测量到的是
连续变量表述的隐形传态
待续…
具体实验实现方案?
隐形传态实验有多种物理实现方案,最常见的应该是光子,因为光子不容易退相干,且具有比较多的自由度来编码量子信息,比如偏振、频率以及路径等。
偏振作为变量
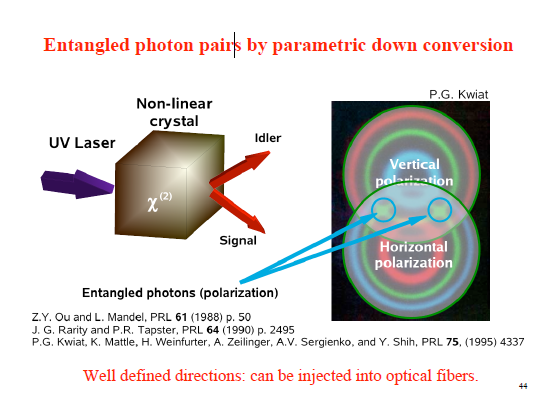
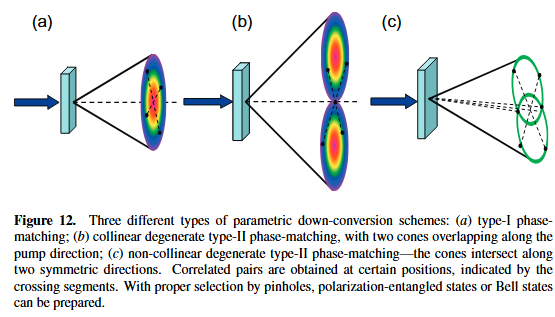
由光子作为理想的纠缠粒子对,假设纠缠的变量是偏振,例如一些非线性材料在光照射时,会产生一对偏振互相垂直的光子对,且传播方向相反,这样偏振的维度就纠缠了起来。
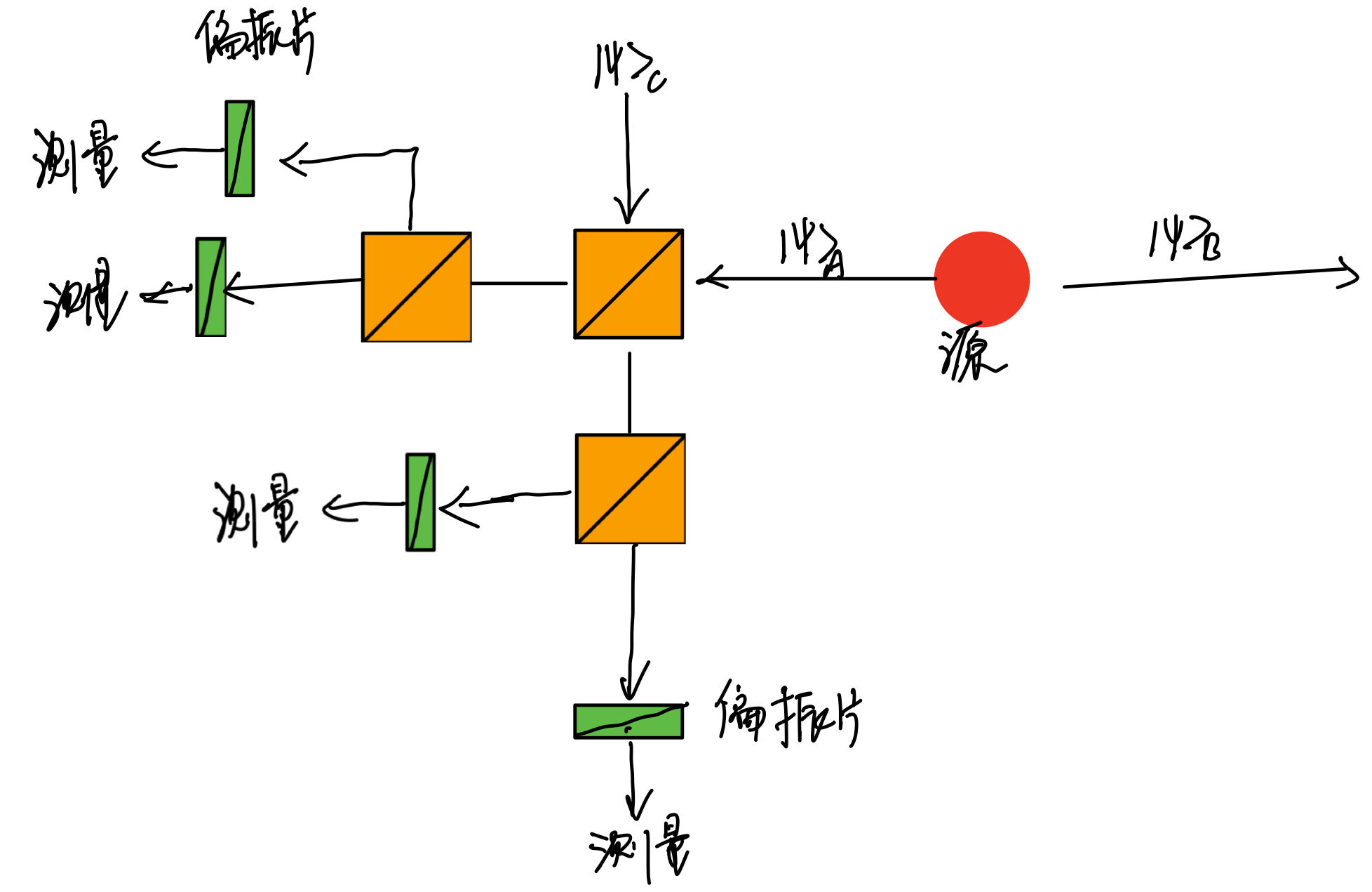
如上图所示,由源产生了偏振互相垂直的两个光子,分别发送到Alice和Bob方向。Alice手中还有一个光子偏振未知,即我们要传输的态。通过一个1/2分束器将来自于源的光子和需要传输的光子混合,然后再作贝尔测量,通过测量结果,判定Bob手中的态应该作何种变换。
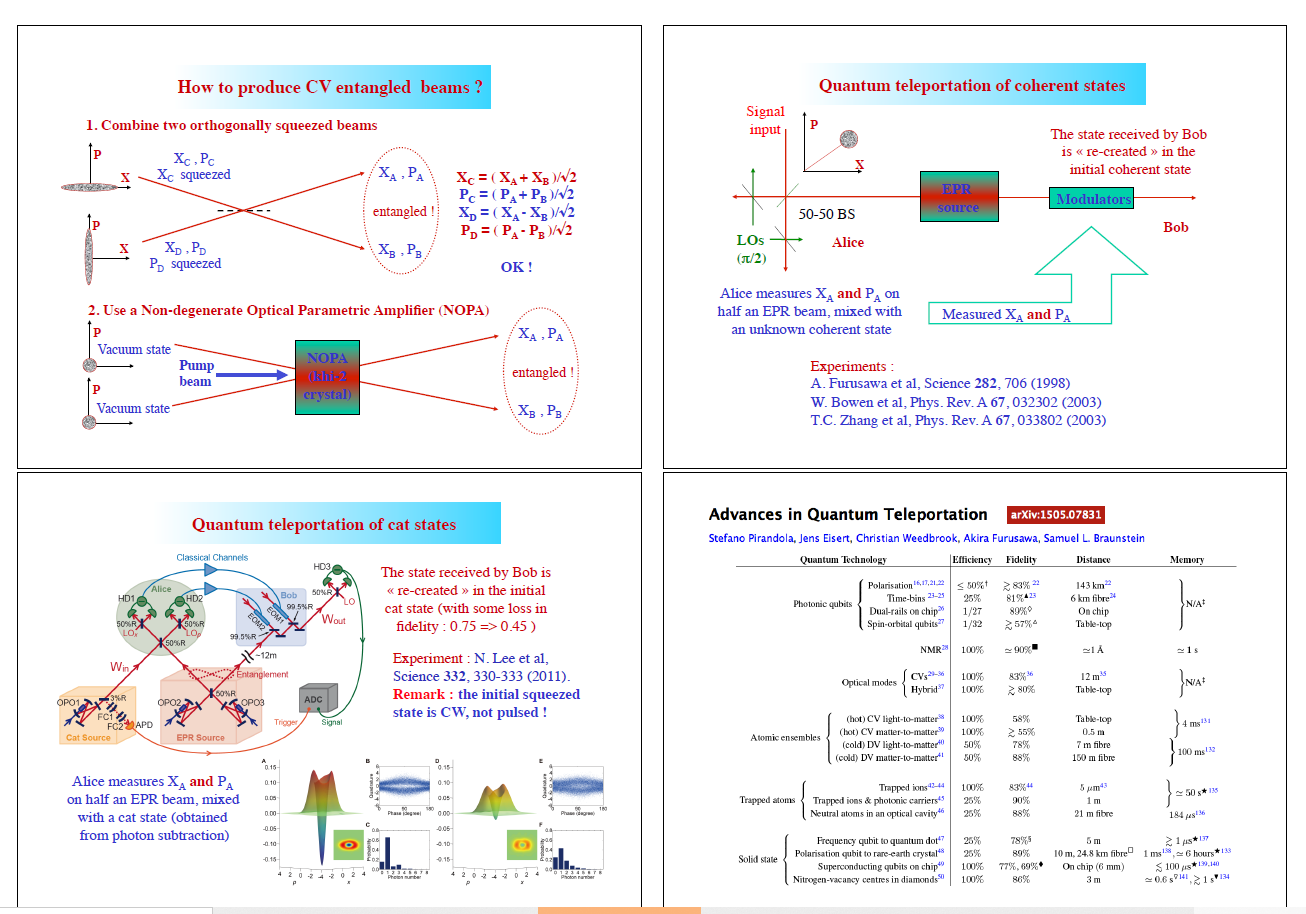
另外还有利用连续变量加密的量子态的隐形传态,我自己还没有完全理解细节,感兴趣的可以查阅Philippe Grangier的文章。