量子计算与量子信息(一)量子计算有关的历史
Quantum #Optics
一直想做一个量子计算的笔记,之前写了一个量子隐形传态的笔记,现在打算将基本历史做一个比较广的总结。
早期计算机的发展

为了方便计算,早在古代,人们就发明了算盘等工具,这算是计算机最早的雏形。
在17世纪的欧洲,诞生了各种简单的机械的计算机,如Schickard在1623年以及Pascal在1642年发明了可以加减的机械计算机,1687年莱布尼兹发明了可以进行乘除运算的机械计算机等。
Charles Babbage在1834年构思、发明出了世界上第一台可编程的机械计算机,该机器包含了算术逻辑单元、控制单元以及集成内存,使其成为通用计算机的第一个设计,因此Charles Babbage被称为通用计算机之父。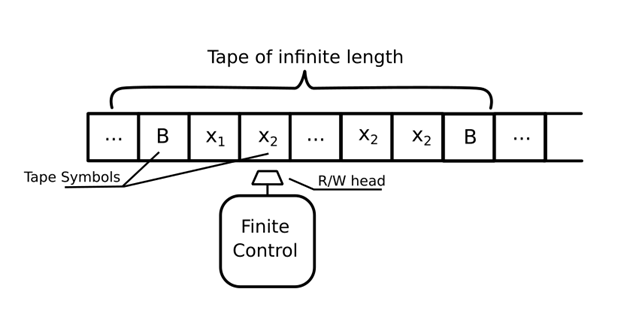
Alan Turing则在上世纪提出了著名的图灵机模型,同时基于对于计算机和人脑的对比,提出了图灵检验,其超前的思想使得他被称为“计算机科学之父”。
大名鼎鼎的冯·诺依曼则提出了冯·诺依曼架构,其将程序和数据一起存储在存储器中,使得早起的简单的硬件编程电子计算机变成了可以软件编程,并亲自参与了1946年的第一台图灵完备的电子数字计算机ENIAC的研制,冯诺依曼也被称为“计算机之父”。
不过世界上第一台电子计算机则是John Vincent Atanasoff在1939年制造的 “ABC机”,其逻辑元件采用的是真空电子管。
1947年12月,贝尔实验室的肖克利等人研制出了一种点接触型的锗晶体管,晶体管出现后,人们就能用一个小巧的、消耗功率低的电子器件,来代替体积大、功率消耗大的电子管了。之后晶体管开始被集成,由此经历了集成电路时代以及大规模集成电路时代。
量子计算的发展

量子计算的概念始于上世纪90年代,当时63岁的物理学家Richard Feynman在一次会议中作出了题为“Simulating physics with computers”的演讲,他提出要模拟计算我们周围的量子世界,仅仅用经典的计算机非常困难的,必须用量子力学的规律来设计计算机[1]。
同时,另外一位俄罗斯数学家Yuri Manin也在他的书中提出了要计算量子多体系统如果用经典的计算机所需的资源将会指数增加。
物理学家则 Paul Benioff[2] 发表了一系列文章提出了图灵机的量子力学模型[2],他证明了对于每一个图灵机和任意数量的问题规模,都存在一个对应的哈密顿量和一类合适的初态,让图灵机的每一步的计算对应到纯态的演化过程中。
David Deutsch在1985年发表了那篇影响深远的文章[3],他提出了加强版的“Church–Turing principle”:任意物理上可有限实现的系统均能被一个通用计算机在有限资源下完美模拟。他指出量子图灵机可以满足加强版的加强版的“Church–Turing principle”,同时他还指出了量子计算机不仅仅可以被用来解决量子问题,由于量子计算的并行性、随机性以及量子关联等,一些经典的问题也可以通过量子计算机得到极大的加速。这些概念都极大的指导了后续计算机科学的研究。
在上述物理学家的启发带领下,量子计算有关的理论、实验相继被做出。
1992年David Deutsch和Richard Jozsa找到了一种特殊的Deutsch–Jozsa算法和问题[10],对于量子计算很容易但是对于经典计算机来说却很困难,证明了量子计算在某些问题上的优越性。
Peter Shor在1994年提出了Shor算法[11],提出了量子计算机在解决质因数分解上的高效性,其速度远胜传统电脑,对于现在通行于银行及网络等处的RSA加密算法可以破解而构成威胁。
Lov K. Grover则在1996年提出了Grover算法[12],用来加速搜索,被公认为即Shor算法之后的第二大经典量子算法。
1998年 Bernhard Omer提出了量子计算编程语言[13],拉开了量子计算机可编程的帷幕。
2000年DiViCenzo提出了实现通用的量子计算机需要满足的五个条件[14]:(1)具有可大规模拓展的高质量的量子比特;(2)量子比特可以被初始化到简单的基态,如
在理论发展的同时,人们开始在各种不同的物理系统中进行量子计算的实现。如NMR[6],超导系统[7]、半导体量子点系统[5],离子阱系统[4]、量子拓扑系统[16,17]以及光学系统等。每一种系统都有各自的优势和缺点,并在目前都取得了进展。同时D-Wave,Intel,IBM,Google、微软等商业公司也纷纷加入了量子计算机的研制。目前最成功的当属超导量子比特,2019年Google公司的研究人员构建了一台由54个量子比特组成的Sycamore处理器[7],其用来进行量子线路采样计算,他们表明该量子处理器在200秒内进行100万次样本采集。2020年,中国科学技术大学的潘建伟院士团队通过光学系统构建了由76个光子组成的量子计算机“九章”[8],对于高斯波色采样进行了快速求解。
什么是计算?
计算是我们人类才有的概念,自然界每天都在不停的演化,我们人类会提出一些抽象的理论模型,来对自然界进行描述,包括对于未来的预测以及历史的探究等,当然描述不是全部描述,只需要将我们关心的物理性质提取出来,比如位置、动量、温度等。这些理论模型往往涉及到一些复杂的逻辑推理和数学运算,比如量子力学就是需要我们来解薛定谔方程,仅仅靠人用笔和纸来进行计算是不够高效的,图灵最早构想图灵机也是想象的有一个机器能够模拟我们人类在纸上进行运算这一活动。
为了能够高效的求解量子问题,最好是用量子图灵机来进行。这样一个量子图灵机的物理实现,可以先用一些抽象简化的物理模型来进行研究,我觉得这些模型主要可以分为两类,一类是波包性质的,即需要传播的,比如光子、声波等(还有一些自旋波这种不是很懂,可能也是抽象出来的准粒子?),其能级是一个连续谱;一类是具体的局域的物理系统或者物质,其能级一般是分离的,包括各种多能级系统、谐振腔、非线性晶体等。用这些抽象的物理模型之间的耦合、能量交换来进行量子计算,也对应着不同的物理平台。
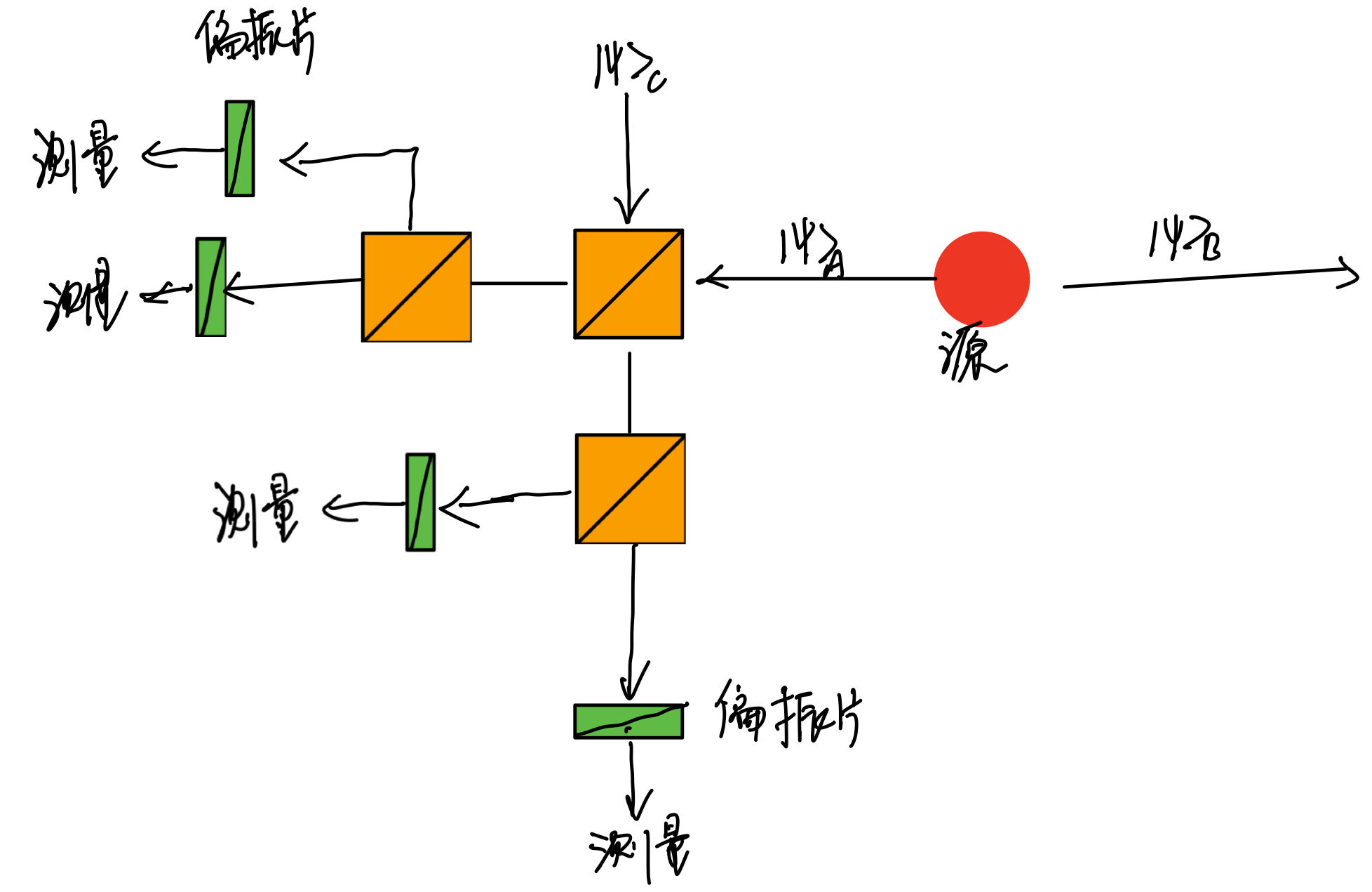
我做了下面的一个示意图来描述量子计算的思路。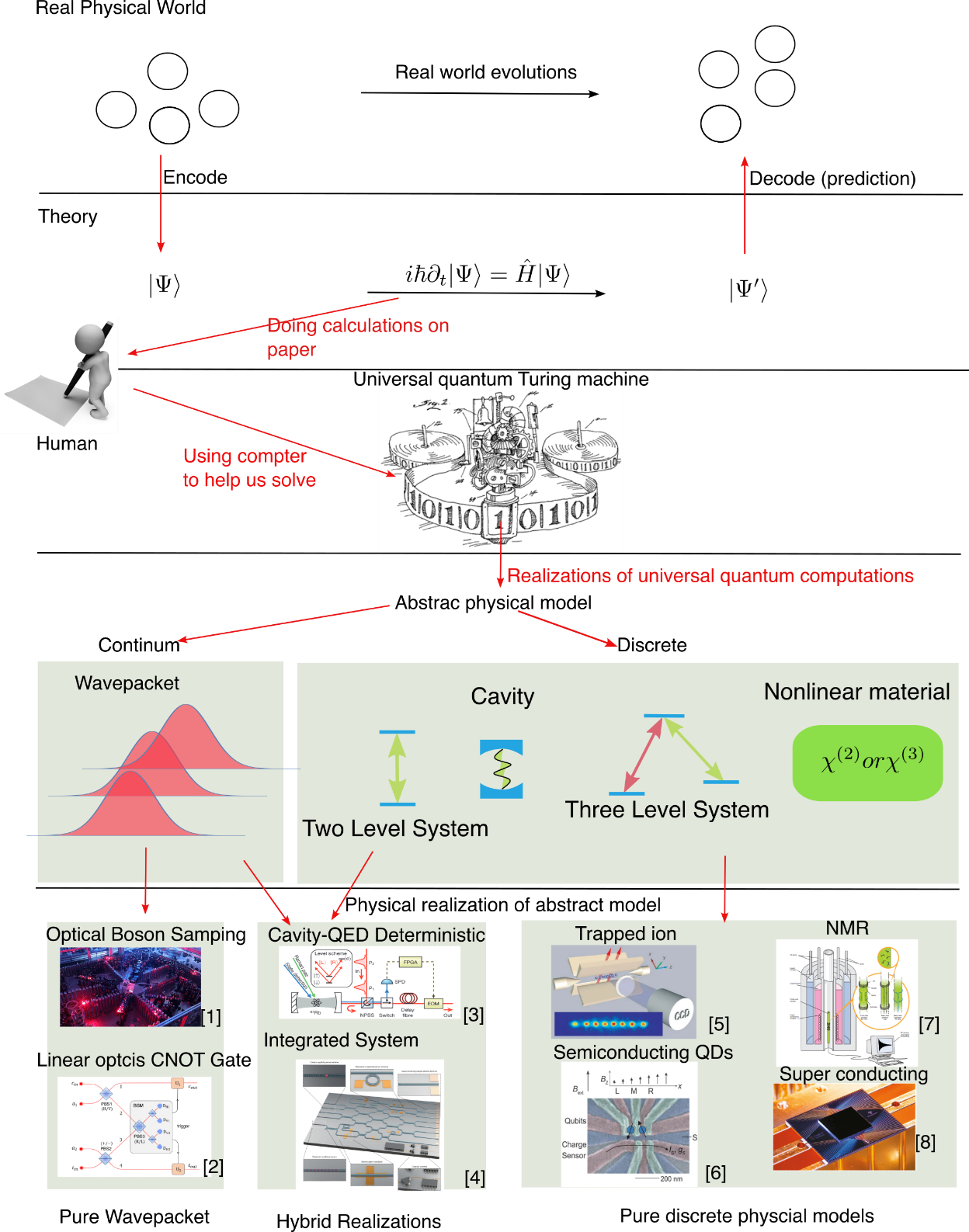
以下是上图的一些参考文献:
[1] H.-S. Zhong, H. Wang, Y.-H. Deng, M.-C. Chen, L.-C. Peng, Y.-H. Luo, et al. Quantum Computational Advantage Using Photons. Science, 2020, 370(6523): 1460–1463
[2] J.-P. Li, X. Gu, J. Qin, D. Wu, X. You, H. Wang, et al. Heralded Nondestructive Quantum Entangling Gate with Single-Photon Sources. Physical Review Letters, 2021, 126(14): 140501
[3] B. Hacker, S. Welte, G. Rempe, S. Ritter. A Photon–Photon Quantum Gate Based on a Single Atom in an Optical Resonator. Nature, 2016, 536(7615): 193–196
[4] E. Pelucchi, G. Fagas, I. Aharonovich, D. Englund, E. Figueroa, Q. Gong, et al. The Potential and Global Outlook of Integrated Photonics for Quantum Technologies. Nature Reviews Physics, 2021: 1–15
[5] R. Blatt, D. Wineland. Entangled States of Trapped Atomic Ions. Nature, 2008, 453(7198): 1008–1015
[6] X. Zhang, H.-O. Li, G. Cao, M. Xiao, G.-C. Guo, G.-P. Guo. Semiconductor Quantum Computation. National Science Review, 2019, 6(1): 32–54
[7] R. Laflamme, E. Knill, D. G. Cory, E. M. Fortunato, T. Havel, C. Miquel, et al. Introduction to NMR Quantum Information Processing. ArXiv:Quant-Ph/0207172, 2002
[8] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature, 2019, 574(7779): 505–510
不同的量子计算模型
对于经典的计算过程,除了图灵提出的图灵机模型以外,还有诸如随机存取机(Random-access machine),布尔电路模型(Boolean circuits),
而量子计算除了同样的量子图灵机模型外,也有量子逻辑门电路(Quantum Circuit)模型,量子退火(Quantum annealing)(或者绝热量子计算)模型、基于测量的量子计算模型(measurement-based quantum computation)以及连续或者分立的量子随机行走模型等。我接下来将会用简要的语言概括其主要思想,因为有一些模型和我们的工作是有交叉的。
1. 量子线路模型 (Quantum circuit model)
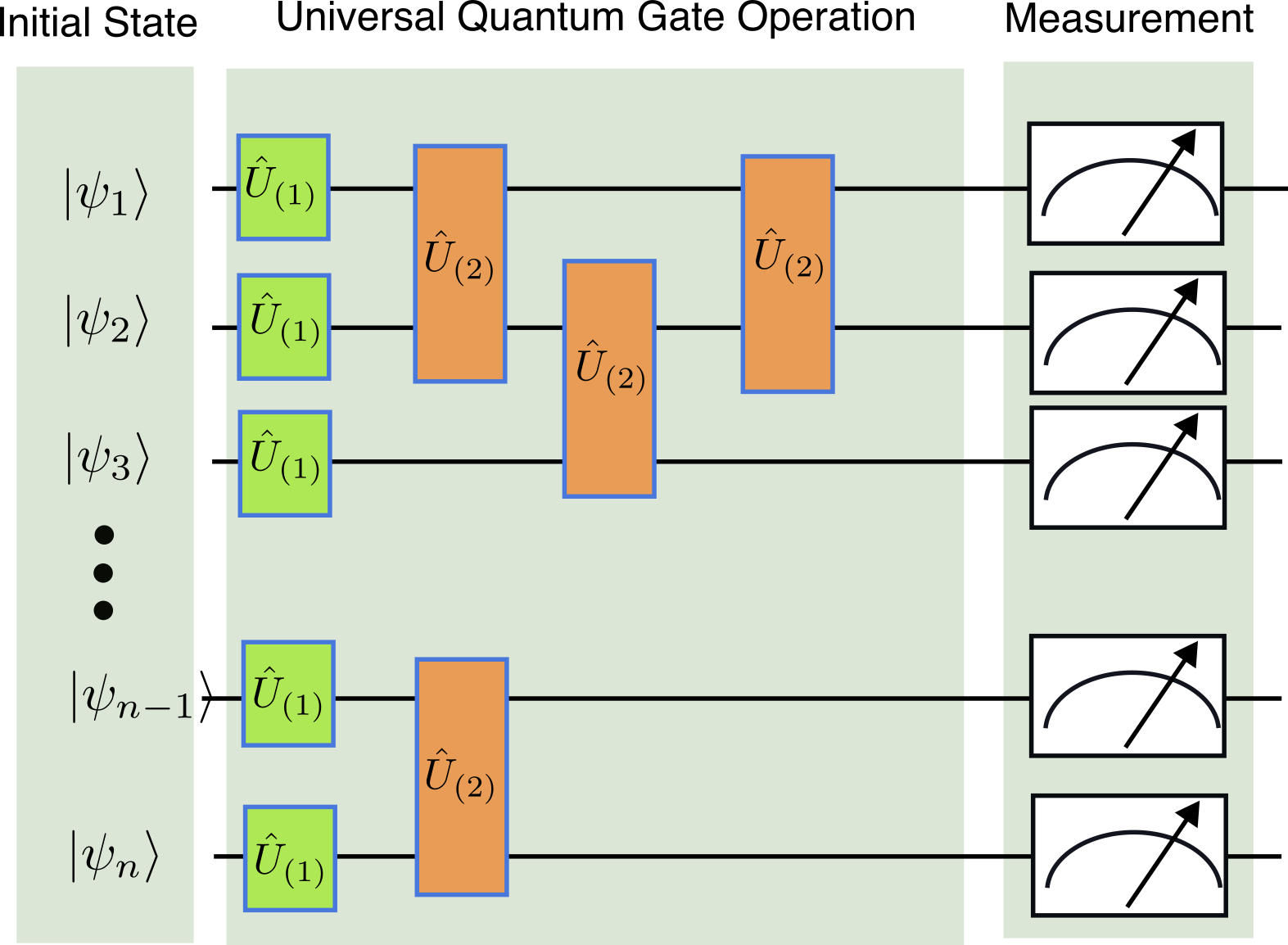
这是一种最常见最熟悉的模型,大家讨论量子计算的时候,也会和经典计算的逻辑电路进行类比,这样更加易于接受。量子逻辑电路模型主要分为三个部分:
- 量子态的初始化
- 通用的逻辑门操作
- 测量
在该量子模型中,除了最后一步测量以外,其他的逻辑门操作都是幺正的、可逆的,这也是大家认为经典计算和量子计算的关键不同点,即基本思路是用一个量子系统的演化去模拟另外一个量子系统的演化,这两个系统的演化都是满足薛定谔方程的。
2. 量子退火模型/绝热量子模型(Quantum annealing or quantum adiabatic quantum computations)
量子计算的过程就是一个系统从初态到末态的幺正演化,而绝热量子演化或者量子退火模型则是需要一个随时间变化的哈密顿量,让系统从初态到末态缓慢的演化,末态刚好是所需要的结果,即我们需要让哈密顿量从初始的!演化到目标的,可以进行如下的设置
3. 基于测量的量子计算(Measurement based quantum computation)
基于测量的量子计算[18],其在2001年提出,其不同之处在于,这篇文章打破了大家的一般的思路,即量子测量一定要是幺正演化的,演化完毕之后再进行相应测量。在该文章中,量子态被初始化到一个非常纠缠的态上,叫Cluster Sate,后续会有一些单比特门的测量,测量比特的顺序、在何种基矢下测量都是要根据所要进行的计算来决定的。
测量的过程中,有一些比特被测量之后,整个量子系统就少了一个比特,还有一些比特被测量之后,可以让另外的比特进行一个隐形传态的过程。
细节部分我可以再单独写一个专门的笔记,这是原文的一些表述:
Here we propose a different model of a scalable quantum computer. In our model, the entire resource for the quantum computation is provided initially in the form of a specific entangled state (a so-called cluster state [6]) of a large number of qubits. Information is then written onto the cluster, processed, and read out from the cluster by one-particle measurements only. The entangled state of the cluster thereby serves as a universal “substrate” for any quantum computation. Cluster states can be created efficiently in any system with a quantum Ising-type interaction (at very low temperatures) between two-state particles in a lattice configuration.
To process quantum information with this network, it suffices to measure its particles in a certain order and in a certain basis. Quantum information is thereby propagated horizontally through the cluster by measuring the qubits on the wire while qubits on vertical connections are used to realize two-bit quantum gates. The basis in which a certain qubit is measured depends in general on the results of preceding measurements. The processing is finished once all qubits except the last one on each wire have been measured. At this point, the results of previous measurements determine in which basis these “output” qubits need to be measured for the final readout. We note that, in the entire process, only one-qubit measurements are required. The amount of entanglement therefore decreases with every measurement [8] and all entanglement involved in the process is provided by the initial resource, the cluster state. This is different from the scheme of Ref. [11], which uses Bell measurements (capable of producing entanglement) to realize quantum gates.
而被大家在光学所广泛引用的则是另外一篇文章,叫做KLM算法。其和上述文章类似的思路,即要实现CNOT门操作,我们需要辅助的纠缠的光子,让纠缠的光子对和目标的光子、控制的光子通过分束器纠缠起来,然后在特定的位置进行测量,只有在一些特定情况下,比如特定分束器端的某个位置都探测到光子,则代表发生的是我们所需的演化,相应的控制门操作完成了,不然就得重新来,或者需要对光子进行操作。
不过对于光子的任意操作,则不需要测量,这是因为对于光子的单比特操作是非常容易的。
4. 量子行走模型 (Quantum walk)
随机行走即假想有一个“walker”在一个“Graph”上进行来回的走动,经典的和量子的随机行走都是初始化一个特定的图之后,然后让粒子随机的在上面漫步,一段时间之后对粒子处于某些位置的概率进行计算,其主要应用领域是一些问题的模拟以及一些搜索算法的实现,后来证明随机行走的量子模型也是和通用的图灵机等价,并可以用来进行通用的量子计算的。
量子的随机行走模型由两种,一种是连续时间的随机行走,一种是非连续的随机行走,主要区别是有没有人在投掷硬币。
Discrete-Quantum walk

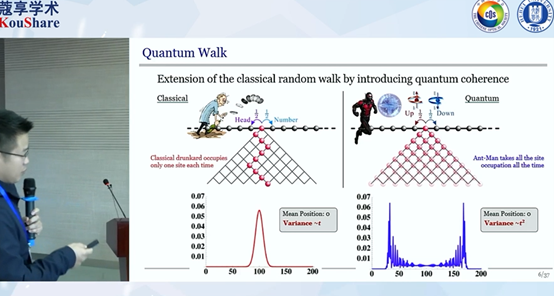
https://www.koushare.com/video/videodetail/8416
如上图所示,是一个一维的随机行走过程,这个人每次都会掷硬币来决定接下来是向左走还是向右走,经典的随机行走只有一条路,但是量子的则是叠加的状态,最后停留位置的最大概率也是不一样的。
通过设计合适的“硬币”和“图”,可以让系统按照我们所需要的方式来演化,实现量子计算。
Viv Kendon[19]在2010年通过和quantum circuit模型对比,证明了这种投掷硬币的量子随机行走是可以进行通用的量子计算的。
Continuous quantum walk

而连续的量子行走则是没有硬币的概念,一个人在一个图决定的哈密顿量下进行连续的满足薛定谔方程的演化,

这里面的主要人物是Childs, 他在2009年首先写了一篇文章证明了连续的随机行走因为可以通用的量子逻辑门而可以完成通用的量子计算[20],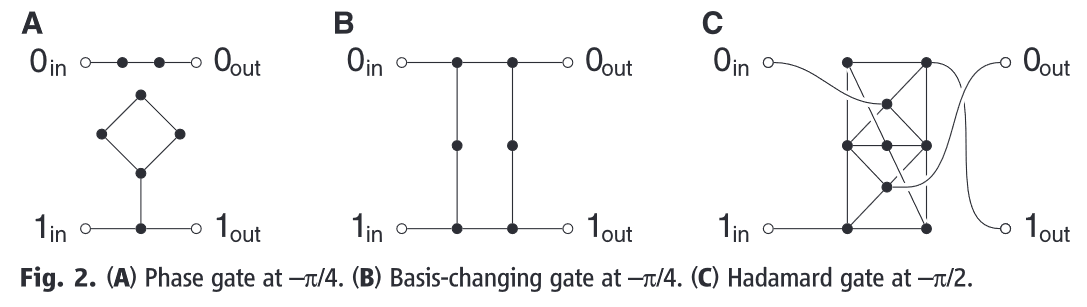
但是这个方法所需的资源很多,比如一个由N个比特组成的系统,其初态有个,然后末态也有个,物理实现的所需要的物理系统很多?
Childs在2013年又写了一篇Science文章,讲述了如何通过多个Walker,Walker之间还可以有相互作用,这样的一个系统来实现随机的量子行走,所需的资源不再是指数的形式。
这些工作Youtube上有一些视频,我看了之后还不能很好的消化。
Viv Kendon自己的报告:
https://www.youtube.com/watch?v=jGyydbJceD0
还有Childs的合作者的报告:
https://www.youtube.com/watch?v=SwOc7kO7acM
但是量子随机行走应该是一种Passive的方式,需要合适的物理系统来实现。
5. 拓扑量子计算(Topological quantum computation)
这是目前还停留在理论的模型,其使用的是一种“任意子”的准粒子来进行量子计算,因为拓扑的保护,这样的量子计算会不容易受到周围环境的干扰而出错。
目前好像就微软在大力的支持该方向的工作。因为对于拓扑的相关知识不是很清楚,所以没有深入研究。
Reference
[1] R. P. Feynman. Simulating Physics with Computers. International Journal of Theoretical Physics, 1982, 21(6): 467–488
[2] P. Benioff. Quantum Mechanical Hamiltonian Models of Turing Machines. Journal of Statistical Physics, 1982, 29(3): 515–546
[3] D. Deutsch. Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer(1985)
[4] R. Blatt, D. Wineland. Entangled States of Trapped Atomic Ions. Nature, 2008, 453(7198): 1008–1015
[5] X. Zhang, H.-O. Li, G. Cao, M. Xiao, G.-C. Guo, G.-P. Guo. Semiconductor Quantum Computation. National Science Review, 2019, 6(1): 32–54
[6] R. Laflamme, E. Knill, D. G. Cory, E. M. Fortunato, T. Havel, C. Miquel, et al. Introduction to NMR Quantum Information Processing. ArXiv:Quant-Ph/0207172, 2002
[7] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature, 2019, 574(7779): 505–510
[8] H.-S. Zhong, H. Wang, Y.-H. Deng, M.-C. Chen, L.-C. Peng, Y.-H. Luo, et al. Quantum Computational Advantage Using Photons. Science, 2020, 370(6523): 1460–1463
[9] J. M. Arrazola, V. Bergholm, K. Brádler, T. R. Bromley, M. J. Collins, I. Dhand, et al. Quantum Circuits with Many Photons on a Programmable Nanophotonic Chip. Nature, 2021, 591(7848): 54–60
[10] D. Deutsch, R. Jozsa. Rapid Solution of Problems by Quantum Computation. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 1992, 439(1907): 553–558
[11] L. M. K. Vandersypen, M. Steffen, G. Breyta, C. S. Yannoni, M. H. Sherwood, I. L. Chuang. Experimental Realization of Shor’s Quantum Factoring Algorithm Using Nuclear Magnetic Resonance. Nature, 2001, 414(6866): 883–887
[12] L. K. Grover. A Fast Quantum Mechanical Algorithm for Database Search. ArXiv:Quant-Ph/9605043, 1996
[13] B. Ömer. A Procedural Formalism for Quantum Computing.
[14] D. P. DiVincenzo. The Physical Implementation of Quantum Computation. Fortschritte Der Physik: Progress of Physics, 2000, 48(9‐11): 771–783
[15] A. W. Harrow, A. Hassidim, S. Lloyd. Quantum Algorithm for Linear Systems of Equations. Physical Review Letters, 2009, 103(15): 150502
[16] A. Yu. Kitaev. Fault-Tolerant Quantum Computation by Anyons. Annals of Physics, 2003, 303(1): 2–30
[17] N. E. Bonesteel, L. Hormozi, G. Zikos, S. H. Simon. Braid Topologies for Quantum Computation. Physical Review Letters, 2005, 95(14): 140503
[18] R. Raussendorf, H. J. Briegel. A One-Way Quantum Computer. Physical Review Letters, 2001, 86(22): 5188–5191
[19] N. B. Lovett, S. Cooper, M. Everitt, M. Trevers, V. Kendon. Universal Quantum Computation Using the Discrete-Time Quantum Walk. Physical Review A, 2010, 81(4): 042330
[20] A. M. Childs. Universal Computation by Quantum Walk. Physical Review Letters, 2009, 102(18): 180501