双粒子系统的非精确量子测量表示

Quantum #Optics

对于两个粒子组成的系统，通过测量掉其中一个粒子，会使得另外一个粒子的状态发生变化。如何用量子力学的语言严格的表述呢？测量有多种类型，假设测量时不精确的呢？这是本篇笔记想要总结的。

单粒子态的测量

在量子力学中，测量过程可以表示为

$$\hat{Q}|q_{i}\rangle=q_{i}|q_{i}\rangle$$

即通过测量，我们可以获得算符的本征值 ,如果量子态处在叠加态

$$|\psi \rangle =\sum _i \psi _i |q_i\rangle ,\psi _i=|\psi \rangle \langle q_i|$$

根据量子力学的原理，我们测量某个量子态，测量得到相应本征态的概率为

$$P_i=\left| \psi _i\right| {}^2$$

同时测量以后，系统也由原来的叠加态塌缩到一个确定的状态

$$|\psi \rangle \longrightarrow |q_i\rangle$$

也可以定义测量投影算符

$$\hat{P}= |q_i\rangle\langle q_i|$$

测量过程的完整表示为

$$\hat{P} |\psi \rangle = |q_i\rangle \langle q_i| \sum _n \psi _n |q_n\rangle=\psi _i |q_i\rangle$$

或者直接写出归一化的末态

$$|\psi \rangle _{\text{measured}}=\frac{\hat{P} |\psi \rangle }{\sqrt{\langle \psi | \hat{P}^{\dagger }\hat{P} |\psi \rangle}}$$

总结一下关键信息:

• 测量的概率就是概率幅的模的平方
• 测量后的量子态需要重新归一化

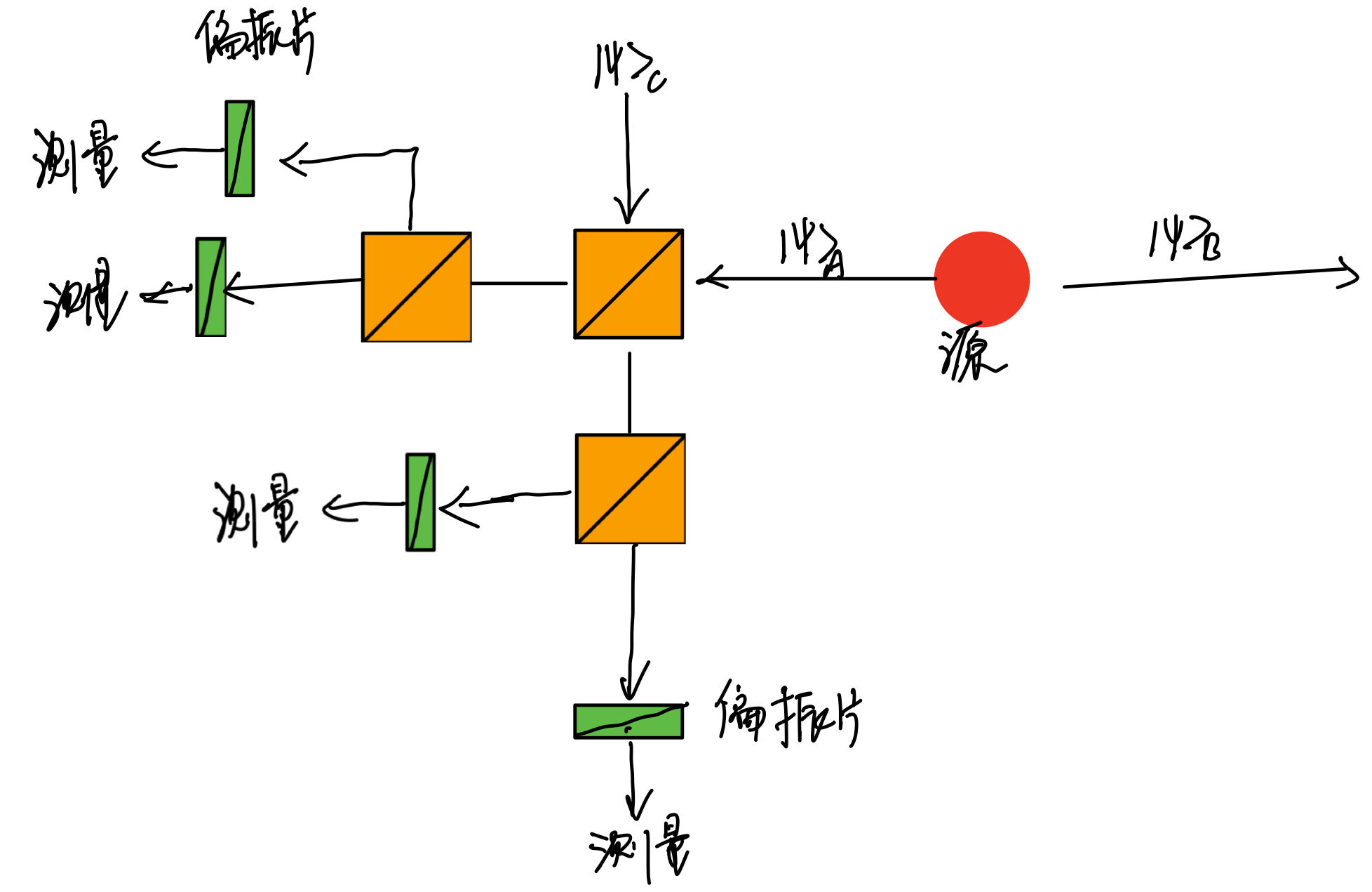
  双粒子态的局域测量

那么对于多粒子态呢？假设考虑两个粒子A，B的量子态，希尔伯特空间表示为 ,量子态表示为

$$|\psi \rangle =\sum _{\mu \nu } \psi _{\mu \nu } |\mu \rangle |\nu \rangle =\sum _{\mu } |\mu \rangle |\phi _{\mu }\rangle$$

其中

$$|\phi_{\mu}\rangle=\sum_{\nu}\psi_{\mu\nu}|\nu\rangle \in \mathcal{H}_{B}$$

和单粒子不同，此时的“系数”是 中的一个矢量 ，此时需要重新定义Partial projector

$$\hat{P}(\mu )=|\mu \rangle \langle \mu |\otimes \hat{I}$$

对双粒子态施加Partial 投影算符可以变为

$$|\psi '\rangle =|\psi \rangle \hat{P}(\mu )=|\mu \rangle |\phi _{\mu }\rangle =\sum _{\nu } |\mu \rangle |\nu \rangle \psi _{\mu \nu }$$

此时的成功率为

$$P_{\mu }=\langle \psi '| |\psi '\rangle =\langle \mu | |\mu \rangle \langle \phi _{\mu }| |\phi _{\mu }\rangle =\sum _{\nu } \left| \psi _{\mu \nu }\right| {}^2$$

测量后的量子态也是需要进行重新归一化

$$|\psi '\rangle =|\mu \rangle \sum _{\nu } |\mu \rangle |\nu \rangle \psi _{\mu \nu } |\phi _{\mu }\rangle \longrightarrow \frac{1}{\sqrt{\sum _{\nu '} \left| \psi _{\mu \nu '}\right| {}^2}}$$

上述测量过程，也可以直接一步到位

$$|\psi \rangle _{\text{measured}}=\frac{\hat{P} |\psi \rangle }{\sqrt{\langle \psi | \hat{P}^{\dagger }\hat{P} |\psi \rangle}}$$

因此，我们测量后，相应的量子态仍然是存在的，只是由原来的叠加态变成了确定性的态。

密度矩阵表示的测量

上述过程，只是表示了特定量子态的测量，实际的物理系统，不一定是纯态，所以用密度矩阵表示是更加一般性的做法，系统的密度矩阵表示为

$$\hat{\rho }=\sum _n \mu _n |\psi \rangle _n\langle \psi _n|$$

那么测量之后(用算符表示)系统的密度矩阵表示为

$$\hat{\rho }'=\frac{\hat{P} \hat{\rho } \hat{P}^{\dagger }}{\text{tr}\left(\hat{P} \hat{\rho } \hat{P}^{\dagger }\right)}=\frac{\sum _n \hat{P} \mu _n |\psi \rangle _n\langle \psi _n|\hat{P}^{\dagger }}{\text{tr}\left(\hat{P} \hat{\rho } \hat{P}^{\dagger }\right)}$$

比如前面所述的两粒子系统，是一个纯态

$$\hat{\rho }=\sum _{\mu } \sum _{\mu '} |\mu \rangle |\phi _{\mu }\rangle \langle \mu '| \langle \phi _{\mu '}|$$

那么我们对粒子1进行测量，测量后的量子态为

$$\begin{aligned} \hat{\rho}^{\prime} & =\frac{\sum_\mu \sum_{\mu^{\prime}} \hat{P}(\mu)|\mu\rangle\left|\phi_\mu\right\rangle\left\langle\boldsymbol{\phi}_{\mu^{\prime}}\right|\left\langle\mu^{\prime}\right| \hat{P}^{\dagger}(\mu)}{\operatorname{tr}\left[\hat{\rho} \hat{P}^{\dagger} \hat{P}\right]} \\ = & \frac{|\mu\rangle\left|\boldsymbol{\phi}_\mu\right\rangle\left\langle\boldsymbol{\phi}_\mu\right|\langle\mu|}{\operatorname{tr}\left[\hat{\rho} \hat{P}^{\dagger} \hat{P}\right]} \end{aligned}$$

此时末态仍然是一个纯态。

非精确测量

我这里真正想要阐述的是，非精确测量，具体的内容可以参见下面的书

Quantum Noise, C.W. Gardiner and P. Zoller Chapter 2.

假设我们的探测精度有限，我们不能区分一些结果，此时我们的测量是投影算符的概率和

$$\hat{M}=\sum _{n=1}^R \alpha _n \hat{P}_n$$

其中R表示总的测量算符的个数,

$$\hat{M} \hat{M}^{\dagger }=\sum _{n=1}^R \left(\alpha _n\right){}^* \left(\hat{P}_n\right){}^{\dagger } \sum _{n'=1}^R \alpha _{n'} \hat{P}_{n'}=\sum _{n=1}^R\left|\alpha _n|^2\hat{P}_n\right.$$

代表了每一种状态下的概率幅，一般需要归一化表示

$$\sum _{n=1}^R \left| \alpha _n\right| {}^2=1$$

此时，我们的测量过程，应该表示为

$$\begin{aligned} & \hat{\rho}^{\prime}=\frac{\hat{M}^{\dagger} \hat{\rho} \hat{M}}{\operatorname{tr}\left[\hat{\rho} \hat{M}^{\dagger} \hat{M}\right]} \\ & =\frac{\sum_{n=1}^R \alpha_n \hat{P}_n \hat{\rho} \sum_{n^{\prime}=1}^R \alpha_{n^{\prime}}^* \hat{P}_{n^{\prime}}^{\dagger}}{\operatorname{tr}\left[\hat{\rho} \hat{M}^{\dagger} \hat{M}\right]} \\ & =\sum_{n=1}^R \sum_{n^{\prime}=1}^R \alpha_n \alpha_{n^{\prime}} \frac{\hat{P}_n \hat{\rho} \hat{P}_{n^{\prime}}^{\dagger}}{\sum_{m=1}^R\left|\alpha_m\right|^2 \operatorname{tr}\left[\hat{\rho} \hat{P}_m\right]} \end{aligned}$$

非精确测量后的子系统

上述推导，通过投影测量的方式，给出了测量后的密度矩阵的表达式，但是我们真正关心的是，测量后，剩下的子系统的状态是什么样的呢？其实此时我们需要再取Partial Trace,还是考虑两粒子系统

$$\hat{\rho }=\sum _{\mu } \sum _{\mu '} |\mu \rangle |\phi _{\mu }\rangle \langle \mu '| \langle \phi _{\mu '}|$$ $$\hat{M}=\sum _{\mu=1}^R \alpha _\mu \hat{P}_\mu$$

那么测量后，密度矩阵为

$$\hat{\rho}^{\prime}=\frac{\hat{M}^{\dagger} \hat{\rho} \hat{M}}{\operatorname{tr}\left[\hat{\rho} \hat{M}^{\dagger} \hat{M}\right]}=\frac{\sum_{\mu=1}^R \sum_{\mu^{\prime}=1}^R \alpha_\mu \hat{P}_\mu \hat{\rho} \alpha_{\mu^{\prime}}^* \hat{P}_{\mu^{\prime}}^{\dagger}}{\sum_m\left|\alpha_m\right|^2 \operatorname{tr}\left[\hat{\rho} \hat{P}_m\right]}=\frac{\sum_{\mu=1}^R \sum_{\mu^{\prime}=1}^R \alpha_\mu \alpha_{\mu^{\prime}}^*|\mu\rangle\left|\phi_\mu\right\rangle\left\langle\phi_\mu\right|\left\langle\mu^{\prime}\right|}{\sum_m\left|\alpha_m\right|^2 \sum_v\left|\psi_{\mu v}\right|^2}$$

对上述表达式取Partial Trace即可得到粒子2的密度矩阵

$$\begin{aligned} & \hat{\rho}_{\text {partial }}=\operatorname{tr}_1\left[\hat{\rho}^{\prime}\right]=\sum_{\mu_3}\left\langle\mu_3\left|\frac{\sum_{\mu=1}^R \sum_{\mu^{\prime}=1}^R \alpha_\mu \alpha_{\mu^{\prime}}^*|\mu\rangle\left|\phi_\mu\right\rangle\left\langle\phi_\mu\right|\left\langle\mu^{\prime}\right|}{\sum_{m=1}^R\left|\alpha_m\right|^2 \sum_v\left|\psi_{\mu \nu}\right|^2}\right| \mu_3\right\rangle \\ & =\sum_{\mu_3=1}^R \frac{\left|\alpha_{\mu_3}\right|^2\left|\phi_{\mu_3}\right\rangle\left\langle\phi_{\mu_3}\right|}{\sum_{m=1}^R\left|\alpha_m\right|^2 \sum_v\left|\psi_{\mu \nu}\right|^2} \end{aligned}$$

如果是精确测量我们可以用下面的表达式

$$\hat{\rho}_{\text {partial }}=\operatorname{tr}_1\left[\frac{\hat{\rho} \hat{P}_\mu}{\operatorname{tr}\left[\hat{\rho} \hat{P}_\mu^{\dagger} \hat{P}_\mu\right]}\right]$$

但是如果是非精确测量，我们不能直接写上述的形式，而是应该用标准写法！。

连续波函数举例

前面考虑的都是分立的系统，现在来考虑连续变量系统，考虑双粒子1,2的波函数

$$|\psi\rangle=\iint \psi\left(x_1, x_2\right)\left|x_1\right\rangle\left|x_2\right\rangle$$

密度矩阵表示为

$$\hat{\rho}=\iiint \int \psi\left(x_1, x_2\right) \psi^*\left(x_1^{\prime}, x_2^{\prime}\right)\left|x_1\right\rangle\left|x_2\right\rangle\left\langle x_2^{\prime}\right|\left\langle x_1^{\prime}\right| d x_1 d x_2 d x_1^{\prime} d x_2^{\prime}$$

如果对粒子1进行测量，用表示

$$\hat{M}=\int_{x_0-\Delta / 2}^{x_0+\Delta / 2}\left|x_1^{\prime \prime}\right\rangle\left\langle x_1^{\prime \prime}\right| G\left(x_1^{\prime \prime}\right) d x_1^{\prime \prime}$$

表示探测器在不同位置的置信度。按照标准的做法，测量后的系统应该表示为

$$\begin{aligned} & \hat{\rho}^{\prime}=\frac{\hat{M}^{\dagger} \hat{\rho} \hat{M}}{\operatorname{tr}\left[\hat{\rho} \hat{M}^{\dagger} \hat{M}\right]} \\ & =\frac{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2}\left|x_1^{\prime \prime}\right\rangle\left\langle x_1^{\prime \prime}\left|G\left(x_1^{\prime \prime}\right) d x_1^{\prime \prime} \iiint \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2^{\prime}\right)\right| x_1\right\rangle\left|x_2\right\rangle\left\langle x_2\right|\left\langle x_1^{\prime}\left|d x_1 d x_2 d x_1 d x_2^{\prime} \int_{x_0-\Delta / 2}^{x_0+\Delta / 2}\right| x_1^{\prime \prime \prime}\right\rangle\left\langle x_1^{\prime \prime \prime}\right| G^*\left(x_1^{\prime \prime \prime}\right) d x_1^{\prime \prime \prime}}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1} \\ & =\frac{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} \int_{x_0-\Delta / 2}^{x_0+\Delta / 2} \iint G\left(x_1\right) G^*\left(x_1^{\prime}\right) \psi\left(x_1, x_2\right) \psi^*\left(x_1^{\prime}, x_2^{\prime}\right)\left|x_1\right\rangle\left|x_2\right\rangle\left\langle x_2^{\prime}\right|\left\langle x_1^{\prime}\right| d x_1 d x_2 d x_1^{\prime} d x_2^{\prime}}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1} \end{aligned}$$

最后对测量的系统取Partial Trace

$$\begin{aligned} & \hat{\rho}_{\text {partial }}=\operatorname{tr}_1\left[\hat{\rho}^{\prime}\right] \\ & =\int\left\langle x_1^{\prime \prime}\left|\left[\frac{\int x_{x_0-\Delta / 2}^{x_0+\Delta / 2} \int_{x_0-\Delta / 2}^{x_0+\Delta / 2} \iint G\left(x_1\right) G^*\left(x_1^{\prime}\right) \psi\left(x_1, x_2\right) \psi^*\left(x_1^{\prime}, x_2^{\prime}\right)\left|x_1\right\rangle\left|x_2\right\rangle\left\langle x_2^{\prime}\right|\left\langle x_1^{\prime}\right| d x_1 d x_2 d x_1^{\prime} d x_2^{\prime}}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1}\right]\right| x_1^{\prime \prime}\right\rangle d x_1^{\prime \prime} \\ & =\frac{\iint_{x_0-\Delta / 2}^{x_0+\Delta / 2} \int_{x_0-\Delta / 2}^{x_0+\Delta / 2} \iint G\left(x_1\right) G^*\left(x_1^{\prime}\right) \psi\left(x_1, x_2\right) \psi^*\left(x_1^{\prime}, x_2^{\prime}\right)\left|x_2\right\rangle\left\langle x_2\right| \delta\left(x_1-x_1^{\prime \prime}\right) \delta\left(x_1^{\prime}-x_1^{\prime \prime}\right) d x_1 d x_2 d x_1^{\prime} d x_2^{\prime} d x_1^{\prime \prime}}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1} \\ & =\frac{\iint_{x_0-\Delta / 2}^{x_0+\Delta / 2} \int_{x_0-\Delta / 2}^{x_0+\Delta / 2} \iint \psi\left(x_1, x_2\right) \psi^*\left(x_1^{\prime}, x_2^{\prime}\right)\left|x_2\right\rangle\left\langle x_2^{\prime}\right| \delta\left(x_1-x_1^{\prime \prime}\right) \delta\left(x_1^{\prime}-x_1^{\prime \prime}\right) d x_1 d x_1^{\prime} d x_1^{\prime \prime} d x_2 d x_2^{\prime}}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1} \\ & =\int_{x_0-\Delta / 2}^{x_0+\Delta / 2}\left|G\left(x_1\right)\right|^2 \frac{\iint \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2^{\prime}\right)\left|x_2\right\rangle\left\langle x_2^{\prime}\right| d x_2 d x_2^{\prime} d x_1}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1} \\ & =\int_{x_0-\Delta / 2}^{x_0+\Delta / 2}\left|G\left(x_1\right)\right|^2\left|\psi_{x_1}\right\rangle\left\langle\psi_{x_1}\right| d x_1 \end{aligned}$$

其中

$$\left|\psi_{x_1}\right\rangle=\frac{\int \psi\left(x_1, x_2\right) d x_2\left|x_2\right\rangle}{\sqrt{\int_{x_0-\Delta / 2}^{x_0+/ 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1}}$$

测量后子系统保真度的计算

最后补充一下保真度的计算，假设目标量子态为

$$\left|\psi_{\text {ideal }}\right\rangle=\int f_{\text {ideal }}\left(x_2^{\prime \prime \prime}\right) d x_2^{\prime \prime}\left|x_2^{\prime \prime \prime}\right\rangle$$

那么保真度，按照定义，应该表示为

$$\begin{aligned} & F=\left\langle\psi_{\text {ideal }}\left|\hat{\rho}_{\text {partial }}\right| \psi_{\text {ideal }}\right\rangle \\ & =\iint f_{\text {ideal }}\left(x_2^{\prime \prime \prime}\right) f_{\text {ideal }}^*\left(x_2^{\prime \prime \prime}\right)\left\langle x_2^{\prime \prime \prime \prime}\left|\hat{\rho}_{\text {partial }}\right| x_2^{\prime \prime \prime}\right\rangle d x_2^{\prime \prime \prime} d x_2^{\prime \prime \prime \prime} \\ & =\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} \frac{\left|G\left(x_1\right)\right|^2}{\text { nor }} \iint f_{\text {ideal }}\left(x_2^{\prime}\right) f_{\text {ideal }}^*\left(x_2\right) \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2^{\prime}\right) d x_2 d x_2^{\prime} d x_1 \\ & =\int_{t_{\text {dec }}-t_R / 2}^{t_{\text {dec }}+t_R / 2} \frac{\left|\int f_{\text {ideal }}\left(x_2^{\prime}\right) \psi^*\left(x_1, x_2^{\prime}\right) d \tau_2^{\prime}\right|^2}{\int_{x_0-\Delta / 2}^{x_0+\Delta / 2} G\left(x_1\right) G^*\left(x_1\right) \int \psi\left(x_1, x_2\right) \psi^*\left(x_1, x_2\right) d x_2 d x_1} d x_1 \end{aligned}$$

或者简化一点

$$\begin{aligned} F & =\left\langle\psi_{\text {ideal }}\left|\hat{\rho}_{\text {partial }}\right| \psi_{\text {ideal }}\right\rangle \\ & =\int_{t_{\text {dec }}-t_R / 2}^{t_{\text {dec }}+t_R / 2}\left|G\left(x_1\right)\right|^2\left\langle\psi_{\text {ideal }}|| \psi_{x_1}\right\rangle\left\langle\psi_{x_1}|| \psi_{\text {ideal }}\right\rangle d x_{1} \end{aligned}$$