物理

差分化表示

天下武功出少林，物理中经典光学问题都全部用麦克斯韦方程组描述，量子力学的关键则是薛定谔方程。很多经典的量子物理模型如无限深势阱、简谐振子等模型，薛定谔方程的解都可以解析的表示，但是大部分物理系统得用数值方法来计算。

本篇笔记将会总结如何通过数值方法分析特定物理系统的本征值以及本征矢量。主要参考了该回答：
Numerical solution to Schrödinger equation - eigenvalues

一维空间中一般薛定谔方程可以表示为：

$i \hbar \frac{\partial}{\partial t} \Psi(x, t)=\left[-\frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2}+V(x, t)\right] \Psi(x, t)$

我们假设势能项不含时间，考虑稳态的薛定谔方程，并且近似认为，此时相应的方程变为

$V(x) \Psi (x)- \psi''(x)=E \Psi (x)$

采用差分方法，格点化为

$\Psi (x_0),\Psi (x_1),\Psi (x_2),\text{...},\Psi (x_M)$

同时二阶求导近似为

$\frac{d^2}{dx^2}\Psi (x)\approx \frac{\Psi (x-d)+\Psi (d+x)-2 \Psi( x)}{d^2}=\frac{\Psi (x_{n-1})+\Psi (x_{n+1})-2 \Psi \left( x_n\right)}{d^2}$

将 $\Psi(x{0}),\Psi(x{1}),…,\Psi(x_{N})$ 写成矩阵形式

$|\Psi\rangle=\left[\begin{matrix} \Psi(x_{0})\\ \Psi(x_{1})\\ \Psi(x_{2})\\ \Psi(x_{3})\\ \cdot \\ \Psi(x_{N}) \end{matrix}\right]$

那么原方程可以写为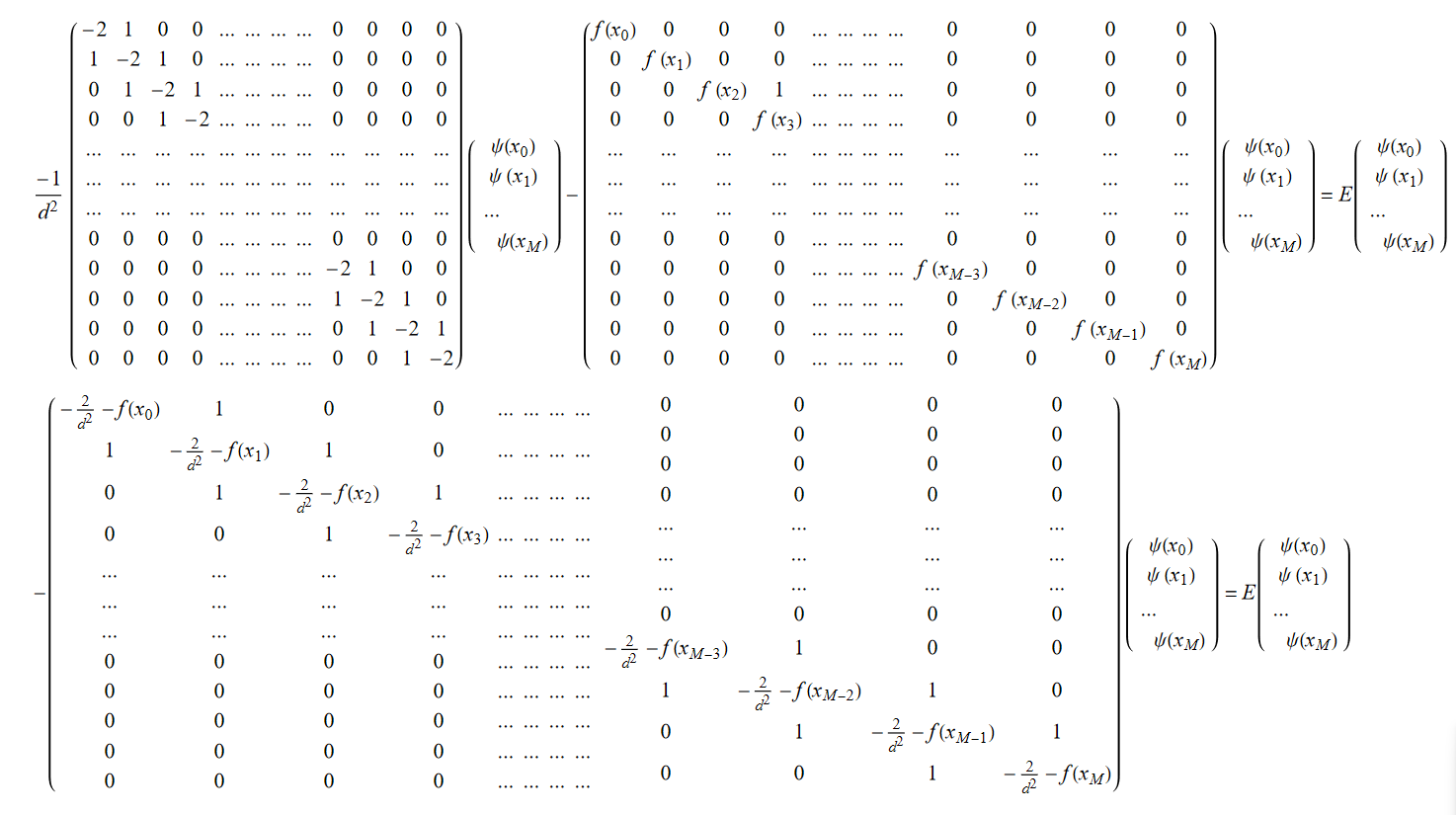

此时可以写为矩阵形式，

$H |\Psi\rangle = E |\Psi\rangle$

此时就是差分离散后的微分方程，通过求解H的本征值，就可以计算量子系统的本质值以及本征矢量了。

无限深势阱模型

现在一无限深势阱模型为例，演示如何通过上述的本征方法数值计算本征模式，并与解析结果进行对比。无限深势阱的势函数为

$V(x)=\left\{\begin{array}{c} \infty, x \leq 0 \text { 或者 } \mathrm{x} \geq L \\ 0,0<x<L \end{array}\right.$

无限深势阱的薛定谔方程可以表示为

$-\frac{\hbar^2}{2 m} \frac{d^2 \psi(x)}{d x^2}+V(x) \psi(x)=E \psi(x)$

其本征函数可以直接写出来

$\begin{aligned} & \psi_n=\sqrt{\frac{2}{L}} \sin \left(\frac{\mathrm{n} \pi \mathrm{x}}{L}\right) \\ & E_n=\frac{n^2 h^2}{8 m L^2}=(2 \pi)^2 \frac{n^2 \hbar^2}{8 m L^2} \end{aligned}$

为了计算方便，令

$\frac{\hbar^2}{2 m}=1$

下面是用Mathematica数值计算的本征值和理论结果的对比，结果是符合的很好的。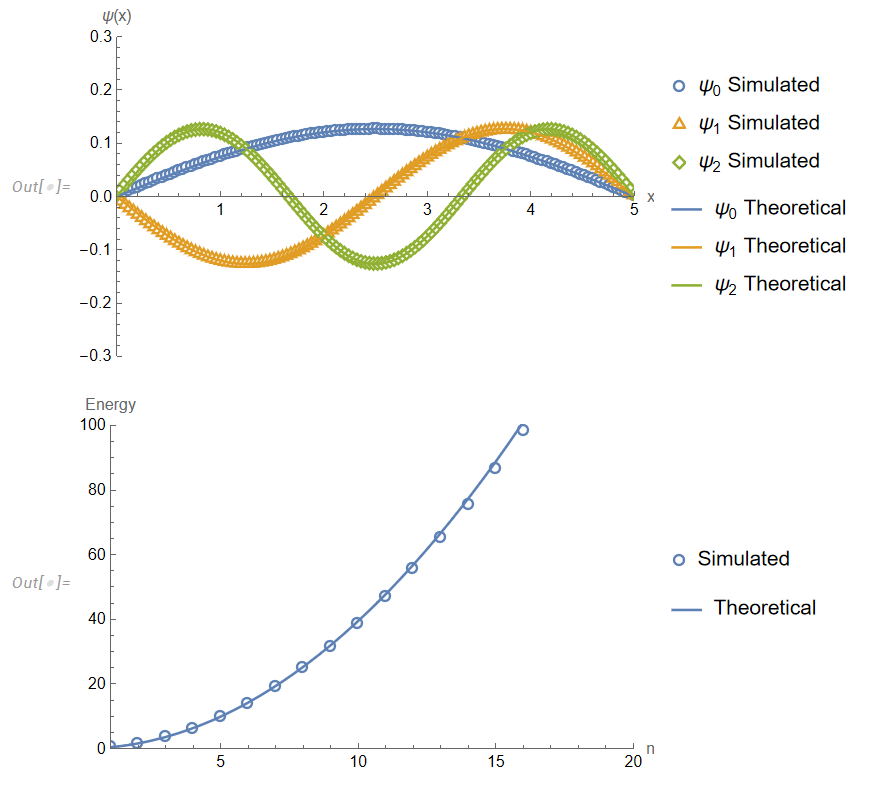

如果将势能改成抛物线形状，也是可以计算的

附录：Mathematica代码

本征矩阵函数

Potential1DMatrix[Vx_,d_]:=Module[{dim,\[ScriptCapitalH],\[ScriptCapitalV],\[ScriptCapitalA]},
dim=Dimensions[Vx][[1]];
\[ScriptCapitalH]=ConstantArray[0,{dim,dim}];
Table[\[ScriptCapitalH][[l,l+1]]=1;\[ScriptCapitalH][[l+1,l]]=1;,{l,dim-1}];
\[ScriptCapitalV]=ConstantArray[0,{dim,dim}];
Table[\[ScriptCapitalH][[l,l]]=-2;\[ScriptCapitalV][[l,l]]=Vx[[l]],{l,dim}];
\[ScriptCapitalA]=-\[ScriptCapitalH]/d^2+\[ScriptCapitalV];
Return[\[ScriptCapitalA]];
]

无限深势阱模型计算

numx = 501;
x = N@Subdivide[-10, 10, numx - 1];
d = x[[2]] - x[[1]];
Vx = ConstantArray[bound, numx];
L = 5;
bound = 1001;
Table[If[x[[l]] < L &&  x[[l]] > 0, Vx[[l]] = 0], {l, numx}];
\[ScriptCapitalA] = Potential1DMatrix[Vx, d];
{\[Lambda]Mat, VecMat} = Eigensystem[\[ScriptCapitalA]];
p1 = ListPlot[{Thread[{x, VecMat[[-1]]}], Thread[{x, VecMat[[-2]]}], 
    Thread[{x, VecMat[[-3]]}]}, PlotMarkers -> "OpenMarkers", 
   PlotRange -> {{0, L}, {-0.3, 0.3}}, 
   PlotLegends -> {"\!\(\*SubscriptBox[\(\[Psi]\), \(0\)]\) \
Simulated", "\!\(\*SubscriptBox[\(\[Psi]\), \(1\)]\) Simulated", 
     "\!\(\*SubscriptBox[\(\[Psi]\), \(2\)]\) Simulated"}, 
   AxesLabel -> {"x", "\[Psi](x)"}];
p2 = ListLinePlot[{Thread[{x, Sqrt[2*d/L]*Sin[\[Pi]/L*x]}], 
    Thread[{x, -Sqrt[2*d/L]*Sin[(2 \[Pi])/L*x]}], 
    Thread[{x, Sqrt[2*d/L]*Sin[(3*\[Pi])/L*x]}]}, 
   PlotRange -> {{0, L}, {-0.3, 0.3}}, 
   PlotLegends -> {"\!\(\*SubscriptBox[\(\[Psi]\), \(0\)]\) \
Theoretical", "\!\(\*SubscriptBox[\(\[Psi]\), \(1\)]\) Theoretical", 
     "\!\(\*SubscriptBox[\(\[Psi]\), \(2\)]\) Theoretical"}, 
   AxesLabel -> {"x", "\[Psi](x)"}];
p3 = Show[{p1, p2}]
p1 = ListPlot[{Sort@\[Lambda]Mat}, PlotRange -> {{1, 20}, {0, 100}}, 
   PlotMarkers -> "OpenMarkers", PlotLegends -> {"Simulated"}
   , AxesLabel -> {"n", "Energy"}];
p2 = Plot[(n)^2/(2*L)^2*4*\[Pi]^2, {n, 0, 21}, 
   PlotLegends -> {"Theoretical"}];
p3 = Show[{p1, p2}]

抛物线形计算

numx = 1001;
x = N@Subdivide[-10, 10, numx - 1];
d = x[[2]] - x[[1]];
Vx = -N@x^4/100;
\[ScriptCapitalA] = Potential1DMatrix[Vx, d];
{\[Lambda]Mat, VecMat} = Eigensystem[\[ScriptCapitalA]];
ListLinePlot[{Thread[{x, VecMat[[-1]]}], Thread[{x, VecMat[[-2]]}], 
  Thread[{x, VecMat[[-3]]}]}]