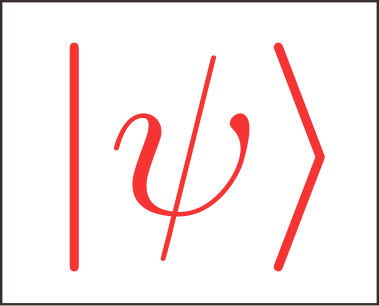Mathematica

目的：

绘制给定直角坐标系下三个垂直的三维箭头，需要绘制出三维效果。

MATLAB没有天然的三维箭头绘制支持，需要用到别人写好的包。我经过多次尝试发现这些包的实现结果都不如人意。最后不得不采用Mathematica来实现，实现的过程中也发现有许多的坑，本篇笔记将会对实现方法进行记录。

角度的对比

用Mathematica绘制时，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Table[
  viewpt = {Sin[\[Theta]view]*Cos[\[Phi]view], 
    Sin[\[Theta]view]*Sin[\[Phi]view], Cos[\[Theta]view]};
  Module[{ thickline = 0.02, thickhead = 0.05},
    
    {d1, d2, d3} = Dipole3DfromRot[{1, 1, 0, 0, 0}];
   
    p2 = Graphics3D[{(*Text[Style["d1",18,Red],d1],*)
          {Red, Arrowheads[thickhead], 
       Arrow[Tube[{{0, 0, 0}, d1}, thickline]]}, {Red, 
       Arrowheads[thickhead], 
       Arrow[Tube[{{0, 0, 0}, -d1}, thickline]]},
          (*Text[Style["d2",18,Red],d2],*)
          {Green, Arrowheads[thickhead], 
       Arrow[Tube[{{0, 0, 0}, d2}, thickline]]}, {Green, 
       Arrowheads[thickhead], 
       Arrow[Tube[{{0, 0, 0}, -d2}, thickline]]},
          (*Text[Style["d3",18,Red],d3],*)
          {Blue, Arrowheads[thickhead], 
       Arrow[Tube[{{0, 0, 0}, d3}, thickline]]}, {Blue, 
       Arrowheads[thickhead], 
       Arrow[Tube[{{0, 0, 0}, -d3}, thickline]]}},
        Boxed -> True, Axes -> False, AspectRatio -> 1, 
     AxesLabel -> {"X", "Y", "Z"}, 
     PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}, 
     PlotLabel -> 
      "\[Theta]=" <> ToString[\[Theta]view/\[Pi]*180] <> ", \[Phi]=" <>
        ToString[\[Phi]view/\[Pi]*180]];
    pexport = 
    Show[p2, ViewPoint -> 3*viewpt, AspectRatio -> 1, 
     ViewProjection -> "Orthographic", 
     AxesOrigin -> {0, 0, 0}]], {\[Theta]view, 
   0, \[Pi]/2, \[Pi]/2/2}, {\[Phi]view, 
   0, \[Pi]/2, \[Pi]/2/2}] // MatrixForm

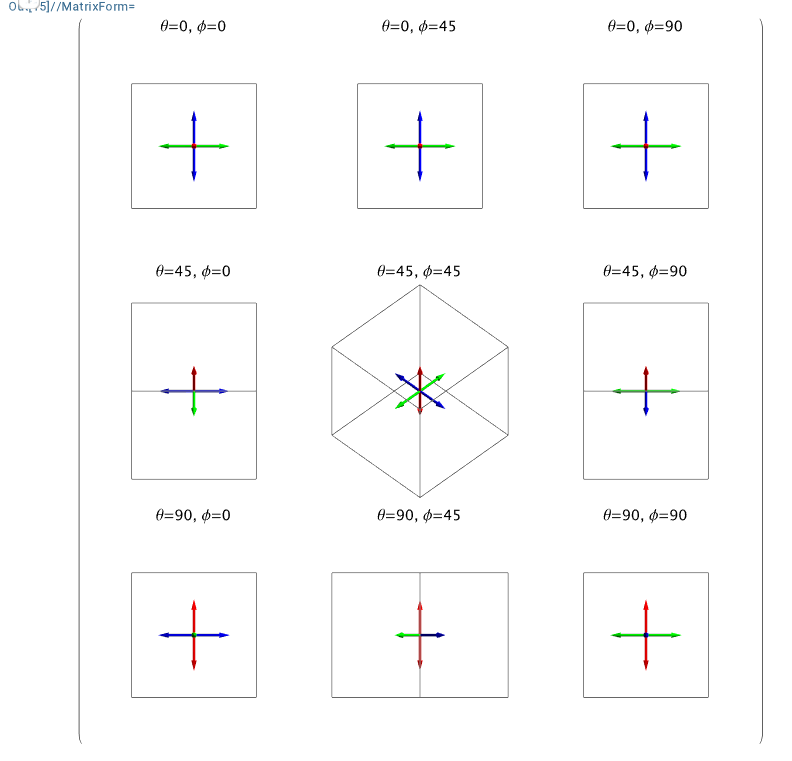
MATHEMATICA

而采用MATLAB时，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
addpath('./FunctionFolder')
[d1,d2,d3]=Dipole3DfromD1Rot([1,1,0,0,0]);
thetamat=[0,45,90];
phimat=[0,45,90];
[thetagrid,phigrid]=meshgrid(thetamat,phimat);
thetagrid1d=thetagrid(:);
phigrid1d=phigrid(:);

figure()
for l=1:9
subplot(3,3,l)
axis equal;
p1=arrow3D([0,0,0], d1/sqrt(sum(abs(d1).^2,'all')),'r');hold on;
p2=arrow3D([0,0,0], -d1/sqrt(sum(abs(d1).^2,'all')),'r');hold on;
p3=arrow3D([0,0,0], d2/sqrt(sum(abs(d2).^2,'all')),'g');hold on;
p4=arrow3D([0,0,0], -d2/sqrt(sum(abs(d2).^2,'all')),'g');hold on;
p5=arrow3D([0,0,0], d3/sqrt(sum(abs(d3).^2,'all')),'b');hold on;
p6=arrow3D([0,0,0], -d3/sqrt(sum(abs(d3).^2,'all')),'b');hold on;
axis equal;
view([phigrid1d(l),thetagrid1d(l)]);
xlabel('x');ylabel('y');zlabel('z');
title(['\theta=',num2str(thetagrid1d(l)),', \phi=',num2str(phigrid1d(l))]);
end

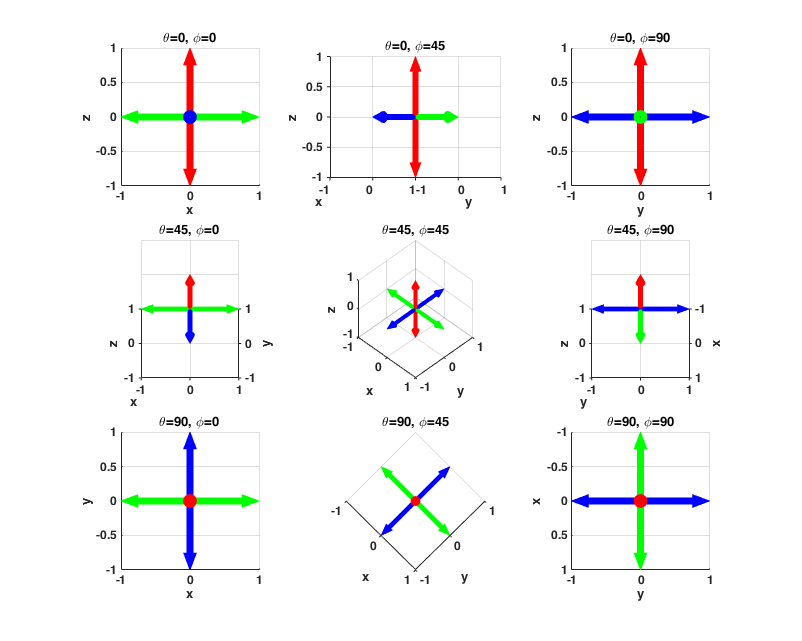
MATLAB
可以看见默认的角度是不一样的，为了角度一致，需要进行调制，变换规则为

调整以后就可以了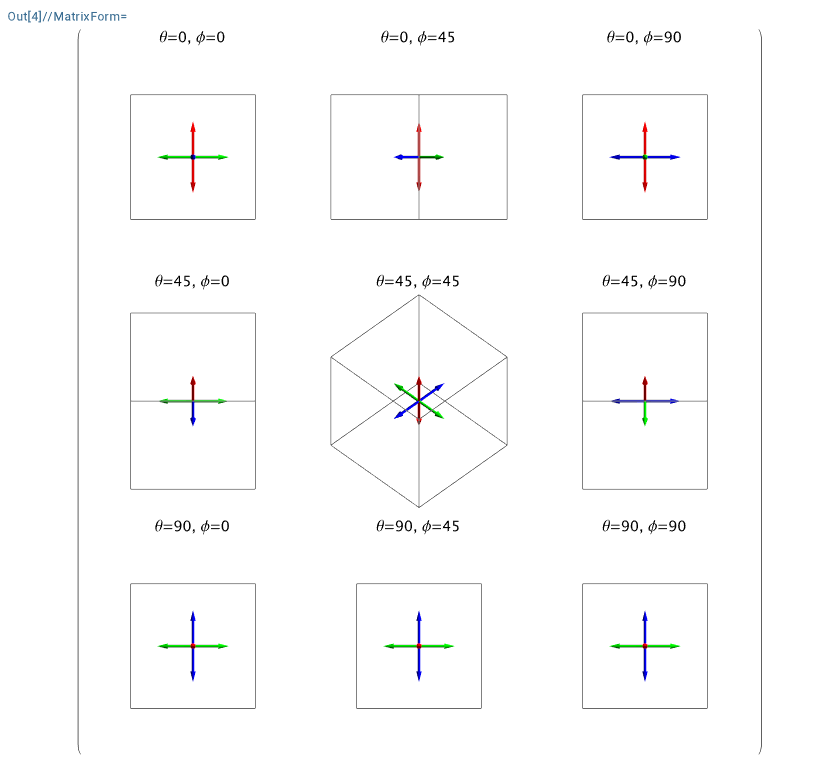
MATLAB

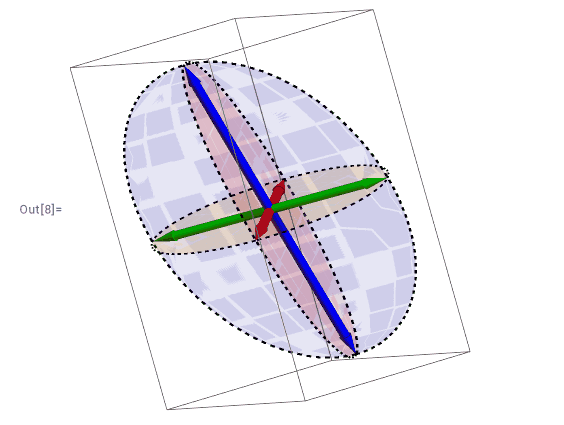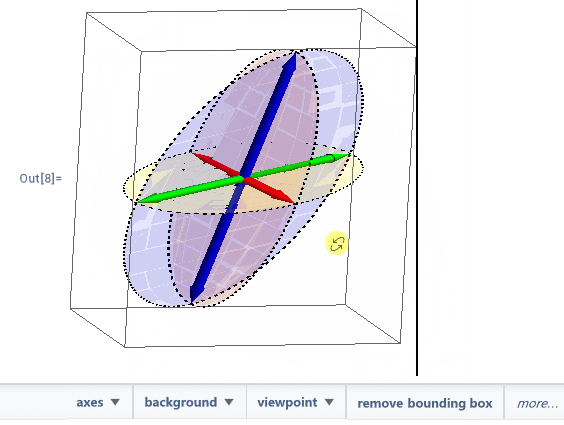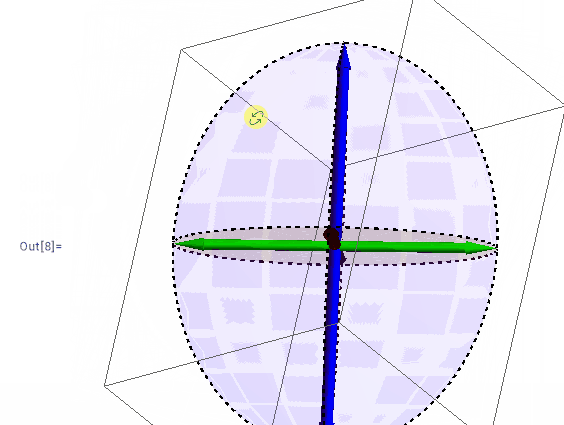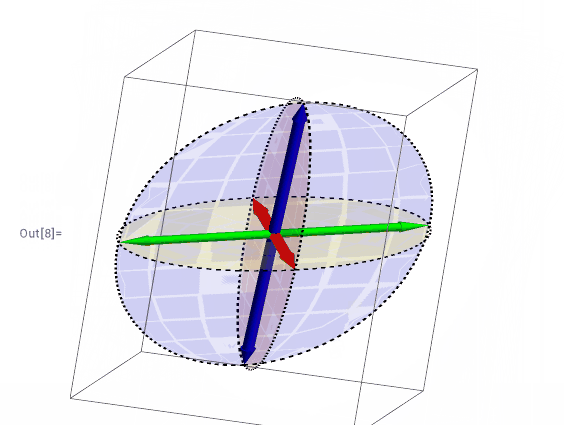
在三个箭头中添加椭圆

还需要添加相应的椭圆，这里设计到三维空间中椭圆的绘制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
parafit = {2, 3, 1, 2, 3};
\[Theta]view = \[Pi]/2; \[Phi]view = \[Pi]/2;
viewpt = {Sin[\[Theta]view]*Cos[\[Phi]view], 
   Sin[\[Theta]view]*Sin[\[Phi]view], Cos[\[Theta]view]};
Module[{\[Alpha] = parafit[[1]], \[Beta] = parafit[[2]], 
  thickline = 0.02, thickhead = 0.05},
 
 dx = N[{1, 0, 0}];
 dy = N[{0, \[Alpha], 0}];
 dz = N[{0, 0, \[Beta]}];
 
 {d1, d2, d3} = Dipole3DfromRot[parafit];
 d1D = Flatten[{d1, d2, d3}];
 dxyz = {Flatten[{dx, dx*0, dx*0}], Flatten[{dx*0, dx, dx*0}], 
   Flatten[{dx*0, dx*0, dx}],
   Flatten[{dy, dy*0, dy*0}], Flatten[{dy*0, dy, dy*0}], 
   Flatten[{dy*0, dy*0, dy}],
   Flatten[{dz, dz*0, dz*0}], Flatten[{dz*0, dz, dz*0}], 
   Flatten[{dz*0, dz*0, dz}]};
 M1D = Inverse[dxyz] . d1D;
 M = ArrayReshape[M1D, {3, 3}];
 p1 = ParametricPlot3D[
   M . {Sin[\[Theta]]*Cos[\[Phi]], \[Alpha]*Sin[\[Theta]]*
      Sin[\[Phi]], \[Beta]*Cos[\[Theta]]}, {\[Theta], 
    0, \[Pi]}, {\[Phi], 0, 2*\[Pi]}, Mesh -> None, 
   PlotStyle -> 
    Directive[Yellow, Opacity[0.1], Specularity[White, 20]],
   Axes -> False , Boxed -> False];
 p1cut = 
  ParametricPlot3D[
   M . {Sin[\[Theta]]*Cos[\[Phi]], \[Alpha]*Sin[\[Theta]]*Sin[\[Phi]],
      0*Cos[\[Theta]]}, {\[Theta], 0, \[Pi]}, {\[Phi], 0, 2*\[Pi]}, 
   Mesh -> None, 
   PlotStyle -> 
    Directive[RGBColor[1, 1, 0], Opacity[0.1], Specularity[White, 20]],
   Axes -> False , Boxed -> False];
 p2cut = 
  ParametricPlot3D[
   M . {Sin[\[Theta]]*Cos[\[Phi]], 
     0*Sin[\[Theta]]*Sin[\[Phi]], \[Beta]*Cos[\[Theta]]}, {\[Theta], 
    0, \[Pi]}, {\[Phi], 0, 2*\[Pi]}, Mesh -> None, 
   PlotStyle -> 
    Directive[RGBColor[1, 0, 0], Opacity[0.1], Specularity[White, 20]],
   Axes -> False , Boxed -> False];
 p3cut = 
  ParametricPlot3D[
   M . {Sin[\[Theta]]*Cos[\[Phi]]*0, \[Alpha]*Sin[\[Theta]]*
      Sin[\[Phi]], \[Beta]*Cos[\[Theta]]}, {\[Theta], 
    0, \[Pi]}, {\[Phi], 0, 2*\[Pi]}, Mesh -> None, 
   PlotStyle -> 
    Directive[RGBColor[0, 0, 1], Opacity[0.1], Specularity[White, 20]],
   Axes -> False , Boxed -> False];
 p1Cir1 = 
  ParametricPlot3D[
   M . {Cos[\[Phi]], \[Alpha]*Sin[\[Phi]], 0}, {\[Phi], 0, 2*\[Pi]}, 
   PlotStyle -> 
    Directive[Dashed, Black, Opacity[1], Specularity[White, 20], 
     Thickness[0.005]],
   Axes -> False , Boxed -> False];
 p1Cir2 = 
  ParametricPlot3D[
   M . {Sin[\[Theta]], 0, \[Beta]*Cos[\[Theta]]}, {\[Theta], 0, 
    2*\[Pi]}, 
   PlotStyle -> 
    Directive[Dashed, Black, Opacity[1], Specularity[White, 20]],
   Axes -> False , Boxed -> False];
 p1Cir3 = 
  ParametricPlot3D[
   M . {0, Sin[\[Theta]]*\[Alpha], \[Beta]*Cos[\[Theta]]}, {\[Theta], 
    0, 2*\[Pi]}, 
   PlotStyle -> 
    Directive[Dashed, Black, Opacity[1], Specularity[White, 20]],
   Axes -> True , Boxed -> True];
 p2 = Graphics3D[{(*Text[Style["d1",18,Red],d1],*)
    {Red, Arrowheads[thickhead], 
     Arrow[Tube[{{0, 0, 0}, d1}, thickline]]}, {Red, 
     Arrowheads[thickhead], 
     Arrow[Tube[{{0, 0, 0}, -d1}, thickline]]},
    (*Text[Style["d2",18,Red],d2],*)
    {Green, Arrowheads[thickhead], 
     Arrow[Tube[{{0, 0, 0}, d2}, thickline]]}, {Green, 
     Arrowheads[thickhead], 
     Arrow[Tube[{{0, 0, 0}, -d2}, thickline]]},
    (*Text[Style["d3",18,Red],d3],*)
    {Blue, Arrowheads[thickhead], 
     Arrow[Tube[{{0, 0, 0}, d3}, thickline]]}, {Blue, 
     Arrowheads[thickhead], Arrow[Tube[{{0, 0, 0}, -d3}, thickline]]}},
   Boxed -> True];
 pexport = 
  Show[(*p1,*)p2, p1Cir1, p1Cir2, p1Cir3, p1cut, p2cut, p3cut, p2(*,
   ViewPoint\[Rule]34*viewpt*), AspectRatio -> 1, 
   ViewProjection -> "Orthographic", AxesOrigin -> {0, 0, 0}, 
   Lighting -> Automatic]]

3D dipole with sphere