Zhaohua Tian's Web

Optics This note documents my implementation of the transfer matrix method (TMM) and the scattering matrix method (SMM) for plane-wave propagation and scattering in one-dimensional multilayer structures. The focus is on a consistent field-amplitude definition and on numerical robustness when dealing with thick layers, evanescent waves, or large refractive-index contrasts. All MATLAB codes discussed here are available in my GitHub repository. The physical problem considered throughout this note i ...

物理问题来源最近在用非正交基矢处理一些问题，发现我之前的认知比较荒谬，所以写下这个笔记记录一下。 对于某个态 ，假设其可以写成三个归一化态基矢的叠加，且需 $|\psi1\rangle, |\psi_2\rangle之间不正交，但是|\psi_3\rangle和|\psi{1,2}\rangle$ 都正交 |\psi\rangle = \alpha_1 |\psi_1\rangle + \alpha_2 |\psi_2\rangle + \alpha_3 |\psi_3\rangle \tag{1}对于正交的基石，其系数通过基矢和 的内积获得 \alpha_n = \langle \psi_n | \psi \rangle \tag{2}我们只关注编号为 1,2 基矢空间的向量长度，因此我们理论上可以定义一个新的向量 |\psi_{1,2}\rangle = \alpha_1 |\psi_1\rangle + \alpha_2 |\psi_2\rangle \tag{3} |\psi\rangle = |\psi_{1,2}\rangle + \langle \psi | \ ...

Interview with Shanhui Fan This interview with Shanhui Fan from Stanford University, USA, was recorded as part of the 2017 international symposium “20 Years Nano-Optics”. Q: What was your research field around the year 2000?A: Around year 2000. I was mostly working on photonic crystals. so uh that was probably at the peak of the photonic crystal research. So i was doing a lot of uh theoretical calculation for photonic crystal and trying to figure out how to use these kind of structures for wha ...

在量子光学中，我们会经常对哈密顿量作基矢变换，使得哈密顿量的形式更加简洁，比如Rotating Frame的变换，或这相互作用表象。我将在这个笔记中对这个变换作简单推导，并给出JC系统的例子来说明如何操作。 Rotating Frame可以看做是线性、幺正的基矢变换Rotating Frame其实就是相当于做了一次线性的、幺正的基矢变换，假设这个变换表示为 ，那么在这个变换下，哈密顿量的变换过程为 H \longrightarrow U H U+i \hbar \dot{U} U^{\dagger}=\tilde{H}从薛定谔方程出发， i\hbar \partial_{t}\psi=\hat{H}\psi由于变换的幺正性，因此，因此可以在薛定谔方程两边同时左乘，并在右边添加单位变换 i\hbar\hat{U}\partial_{t}\psi=\hat{U}\hat{H}(\hat{U}^{\dagger}\hat{U})\psi根据求导规则 \partial_{t}(\hat{U}\psi)=\partial_{t}(\hat{U})\psi+\hat{U}\partial_ ...

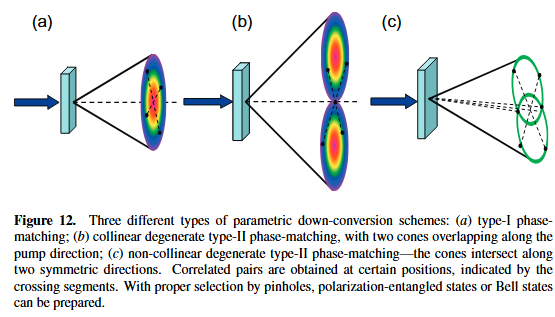
Quantum #Optics本人的研究领域一直是和光子的时域波形有关，因此也需要将目前光量子系统中的常见光子波形进行一个总结。目前的单光子源类型可以分为三类ref1 ： 衰减激光 预报光子 On-demand的单光子源下面分别进行简单的说明。 1） 衰减激光 产生单光子源的最简单的方法是，将激光不断的衰减，使得其光强非常弱，最后只剩下一两个光子。激光是一种经典光，用相干态 ，当时我们近似认为其是一个Fock态的单光子，即 |\alpha\approx 1\rangle\approx |1\rangle当然，相干态的光子性质和真正的Fock态光子还是有很大区别的，这样的光子的品质也不够好。这种衰减激光产生的光子，时域波形就是激光的波形，一般近似用高斯波形来描述。 2）预报类型的单光子源第二类被广泛采用的是，预报类型的单光子源。这类光子源需要先产生纠缠的光子对，通过测量光子对中的一个光子，从而预报另外一个光子的存在。产生的光子，往往是频率纠缠、路径纠缠、偏振纠缠的。产生纠缠光子对的物理过程主要有四波混频和参量下转换。 SPDC过程最早采用的产生光子对的方法是SPDC过程，利用二阶非 ...

写作 #文章本人是一个容易犯错的人，低级错误很多，关键错误也不少。这些错误，给我造成了各种困扰、麻烦，也不能保证在将来不会让我粉身碎骨。 我的标题是如何减少，而不是 如何避免，因为我已经知道，错误是不可避免的。我非常想避免这些错误，所以用这个笔记，来让自己梳理一下，如何才能避免各种各样的错误。 生活中我还有其他的各种错误，这里我主要想强调的是科研中的错误。当然，要避免错误，就得从生活中的一些小事情做事，做到尽量严谨、滴水不漏。 如何改正心态：人非圣贤、孰能无过不要潜意识一直认为自己是一个容易犯错的人一个人，一旦给自己心里暗示，自己哪哪不好，自己的一些不合理的行为，就会变得心安理得。 一定是，要在心里把自己想象成一个，非常认真、仔细的人。 有这样正向的、积极的暗示，你才能做的更好。 要相信即使是计算机也会有Bug，也会罢工，人不是机器，都会犯错就像这次巴黎奥运，也会弄错国旗、国歌；大学生的录取通知书，也会有错别字。 世界是一个巨大的草台班子。 文章不能保证没有任何小问题，特别是公式多、文献多、文字多的文章。 所以，出错不是自己一个人的问题，而是一个普遍规律，就像墨菲定律所说的那样，错误如 ...

写作 #文章每次写好文章后，都需要再仔细校对、检查，防止出错。但是每次从头读到尾，是最耗时间也最低效的一种做法。更加高效的做法应该是，按照下面的步骤来进行检查 [ ] 先整体读一遍，看看是否OK，找出明显的错误 [ ] 语法错误 [ ] 单词拼写错误 [ ] 各种typo [ ] 带着目的的去检查特定位置、关键位置 [ ] 图是不是排布美观、标号是否有问题、Caption是否准确 [ ] 参考文献是否引用合理、正确 [ ] 图的引用是否正确？ [ ] 公式是否正确 [ ] 作者姓名、机构、邮箱、致谢部分 [ ] 出现的每一个字符是不是都进行了说明？ [ ] 从不同的角度来审视自己的文章 [ ] 逻辑是否顺畅 [ ] 核心观点有没有在关键位置点清楚

写作 #文章注意标题是，如何提升文章质量，而不是从头写文章。 如何更好地从头写文章，可以参见另外的笔记[[Physics/E物理文章写作经验总结|E物理文章写作经验总结]] 我这里要总结的是，如何将一篇已经写好的文章进行修改。 修改，其实是非常难的，因为人都是有惰性的。当你重复的读自己的文章的时候，总是顺着原来的思路来读，就很难跳出本来的错误框架。实际上，当你很久以后再来看自己的文章，就会发现有很多地方不好。但写文章需要速度，你没有那么多时间来等待脑子冷却。所以我们需要一些可以操作的方法或者技巧来自己找出文章的问题。 “当你手里有一把锤子，你就希望到处都是钉子，这样你就可以挥舞你的大锤”。 所以我们可以带着下面的问题去检查文章： 是否足够精简？ 是否通俗易懂？ 是否逻辑连贯？ 是否中心突出？ 是否在关键点总结好？ 是否点的清晰，而不是不够明确。 心理上，要告诫自己： 目前的每一步都值得质疑，不要太爱惜自己写好的东西，要大胆狠心的去改变。 学会角色扮演： 你自己如何评价你的文章？觉得自己的哪些要点还没有讲述清楚？ 如果是一个陌生人，第一次看你的文章，会怎么样评价？

写作 #文章投稿文章非常关键的一步就是对审稿人的意见进行回复。下面对Response的一些关键点做一个梳理： 别人问什么，你就答什么，不要顾左右而言它。 对于别人的一些负面疑问，你要展现的是： 我有认真的思考过审稿人提的这个问题，然后才来回答。 我回答的很在点上，且很全面。 为了解决审稿人的这个点，我们做了哪些修改 回答的时候，要逐条回答，也就是point by point 文件格式要清晰好看，可以一眼看清楚，哪一部分是审稿人的问题，哪一部分是你的回答，哪一部分是你的修改。 学会用粗体、特殊颜色等方式，标注清楚，哪些是审稿人特别关心的问题，但是也不要到处都是粗体。 对于比较负面的评价： 表达观点，不同意 理由： 文字表述 公式、数据支持 文献文献支持 结论 面对审稿人的疑问，回答的时候，要保持合适的度： 如果审稿人问你一个你不太了解的问题，也要想办法尽量了解背景，多写一点，证明你不是敷衍了事。 如果审稿人问你一个你擅长的问题，你也不能：过度发挥。审稿人问你A，你说A ,B，C我们都知道，这样很容易又引起新的问题，既没有展示你的博学，还让人觉得你是个半吊子，抓不住重点。 ...

Quantum #Optics对于两个粒子组成的系统，通过测量掉其中一个粒子，会使得另外一个粒子的状态发生变化。如何用量子力学的语言严格的表述呢？测量有多种类型，假设测量时不精确的呢？这是本篇笔记想要总结的。 单粒子态的测量在量子力学中，测量过程可以表示为 \hat{Q}|q_{i}\rangle=q_{i}|q_{i}\rangle即通过测量，我们可以获得算符的本征值 ,如果量子态处在叠加态 |\psi \rangle =\sum _i \psi _i |q_i\rangle ,\psi _i=|\psi \rangle \langle q_i|根据量子力学的原理，我们测量某个量子态，测量得到相应本征态的概率为 P_i=\left| \psi _i\right| {}^2同时测量以后，系统也由原来的叠加态塌缩到一个确定的状态 |\psi \rangle \longrightarrow |q_i\rangle也可以定义测量投影算符 \hat{P}= |q_i\rangle\langle q_i|测量过程的完整表示为 \hat{P} |\psi \rangle = |q_i ...